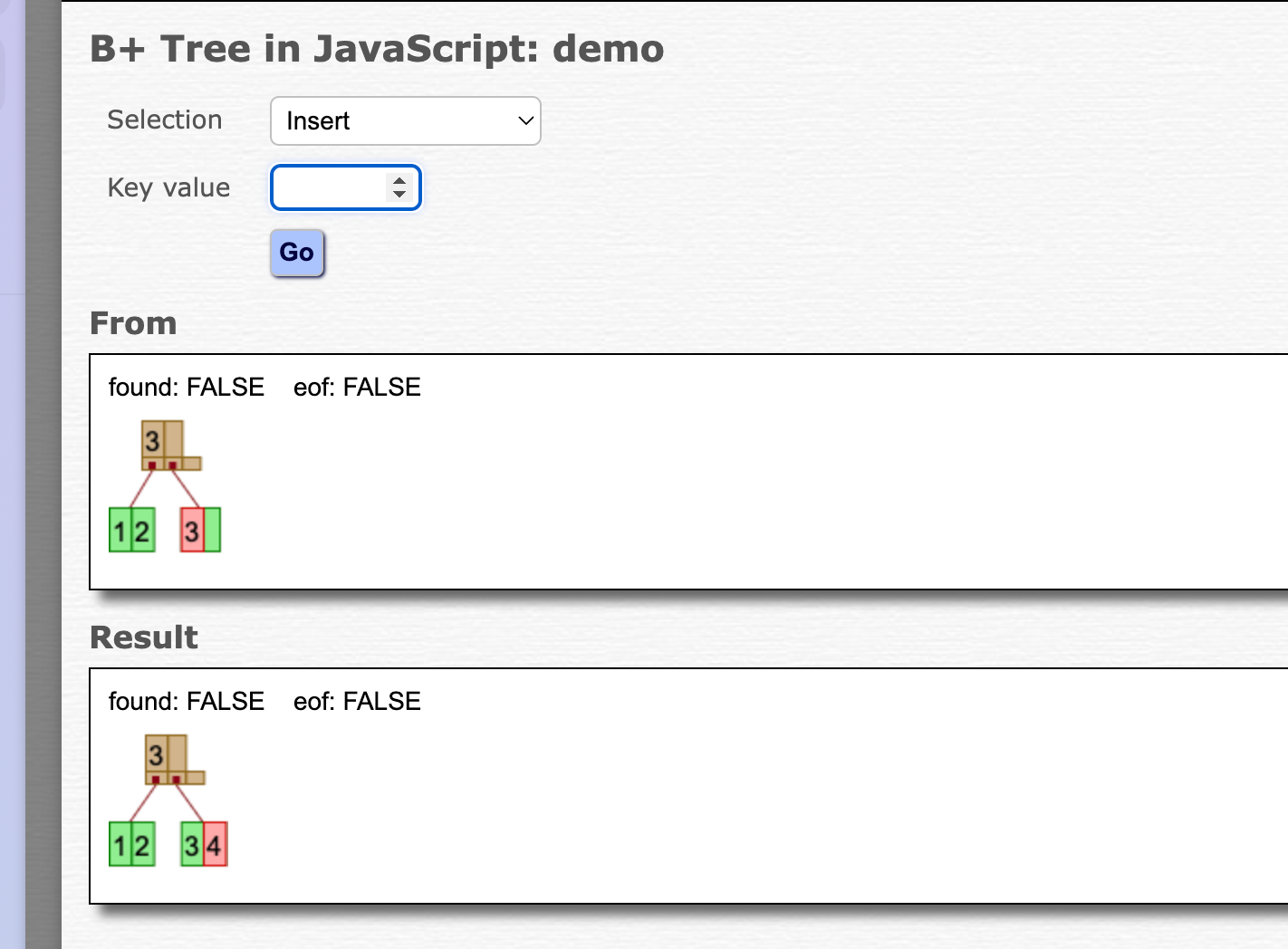
Lab2

对于Lab的debug，由于并没有开放测试样例，因此最好的就是找一个合适的b+树的模拟动画，然后再使用官方的画图工具比较自己的B+树，一般3-4层没有问题了大多就是没有问题了，把分裂、合并、重分配等各种情况全部涉及到一次基本就可以了。

B+树演示动画推荐官方的，其他的可能多少都会有点bug或者实现方式不太一样

https://15445.courses.cs.cmu.edu/fall2022/bpt-printer/

Task1

分别实现 Parent Page Internal Page Leaf Page，按照注释实现即可，较为简单

注意一下arrry_[1]的使用方式即可

flexible array

这里可以参考十一大佬的解释，描述的非常详细：flexible array

array_[1]所采用的是一种flexible array的实现方式，即不指定一个数据的大小，将其封装到一个对象当中，对整个对象分配一个确定的大小，除去已经使用的空间，剩余的空间均可为array_[1]所使用。

对于一个Internal Page，BUSTUB_PAGE_SIZE定义的为4KB，即4096B，除去从父类继承而来的6个字段各占4B，其他剩余的所有内存均供flexible array来使用

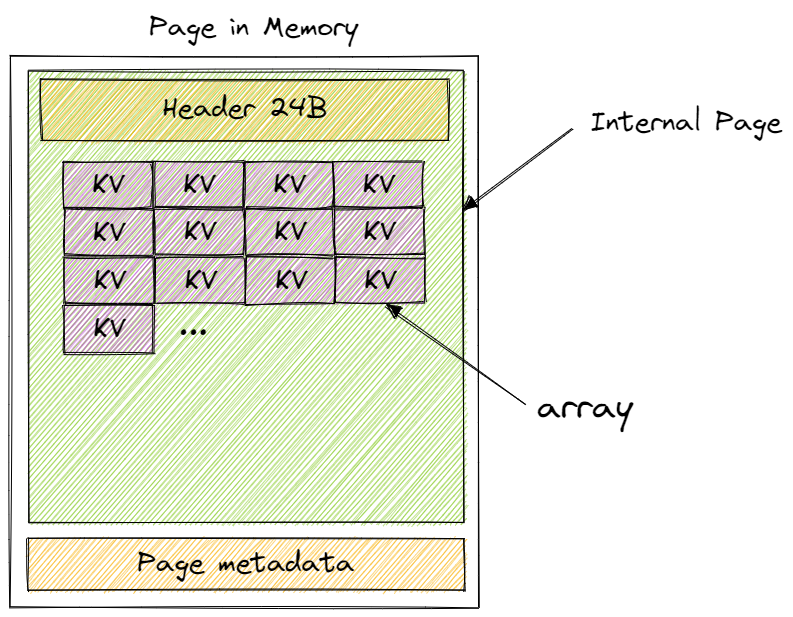
Page and BPlusTreePage

就像上面的图画的那样，这二者之间并不存在继承或者实现的关系，二者在类的定义上为并列的关系，并不像是在6.830的simpledb 当中通过BPlusTreePage去实现Page接口。

B+树的一个Page作为索引而存在，而叶子节点即是索引又是真实的存储单元（即存储Tuple对应的RID，非聚簇索引实现）。

即当要读取一个tuple时，首先根据保存的root_page_id去找到根节点，通过buffer_pool_manager将其加载到内存当中，而root_page是作为Page的数据维护在内存当中，Page当中的data_为一个4KB的字节数组，通过reinterpret_cast将其重新解释为BPlusTreePage，后续在其中搜索到对应的Key，在通过buffer_pool_manager去找到下一个节点，直至最后找到叶子节点，并通过RID再去读取到tuple。

而对于HeapFile的实现方式，则是找到一个表的HeapFile，然后遍历不断读取其中的HeapPage，通过bufffer_pool_manager将其加载到内存当中，再遍历HeapPage当中的所有的tuple，直至找到对应的tuple。

节点实现

节点大小

先说一个数据库系统概念当中对大小的定义：

首先对于内部节点和叶子节点的大小都基于Max Degree n

对于叶子节点max_size为n-1个kv，min_size为(n-1)/2向上取整
对于内部节点max_size为n个指针，n-1个k，min_size为n/2向上取整个指针

在Lab当中，对于一棵B+树，并没有制定Max Degree，而是分成leaf_max_size和internal_max_size来定义的，可以分开设置但是二者理论上应该是相等的：在是否需要分裂的判断时，Lab给出的逻辑是：internal_max_size在插入前进行判断，leaf_max_size在插入后进行判断，因此即可保证内部节点可以比叶子节点多容纳一个指针。

因此对于min_size的求法：

leaf_node: n / 2
internal_node (n + 1) / 2

不减一直接除可以与-1之后向上取整等价。

实现方式

在一个Page内部通过array_[1]来保存所有的KV，array_[1]的元素类型为一个KV键值对，对于叶子节点的实现较为便捷，kv的数量相等，直接从头开始填充即可，在bustub所实现的为非聚簇索引，因此key即为设置索引的键，value即为RecordId。在通过索引找到了RecordId之后再使用RecordId在一个Page当中去进行偏移读取。

如果想MySQL那样的话主键索引锁存储的为整个tuple，二级索引存储的则是索引和主键，通过二级索引进行查询，需要通过一个回表的过程。

‍

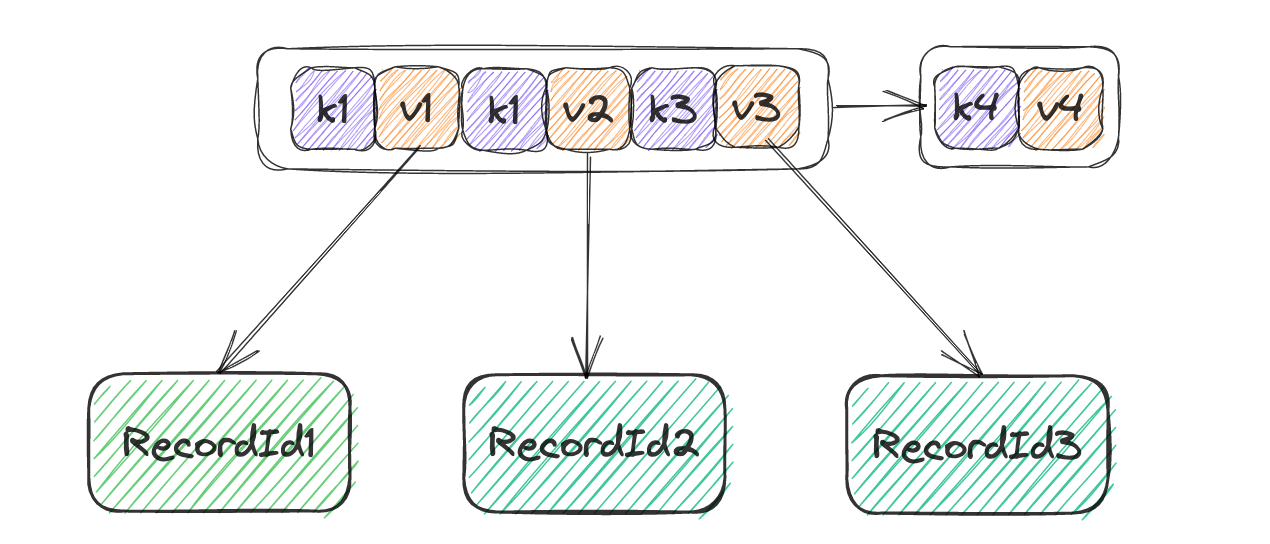
而对于internal_page的实现稍微复杂一点，由于指针比索引多一个，因此可以选择将第一个key标记为空，不存储任何东西，之后再更新索引的时候记得跳过0号位，从1开始。

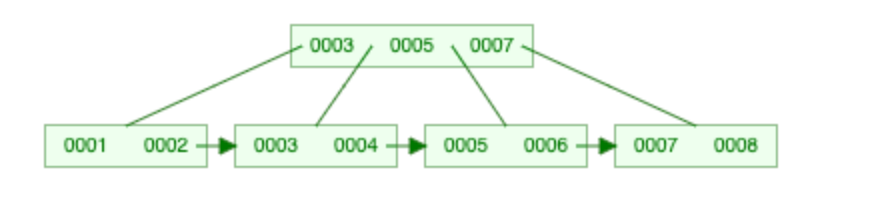
对于上图的0003 0005 0007则为：

Task2

只支持唯一索引，当插入重复的key时需要不执行并返回false。

在插入时需要进行最大值的检测：

对于内部节点为插入前子节点的数量（指针的数量）等于max_size
对于叶子节点为插入后kv键值对的数量等于max_size

写操作可能会导致根节点的更新，使用updateRootPageId进行更新，只要root_page_id需要更新时，就对其进行调用

GetValue

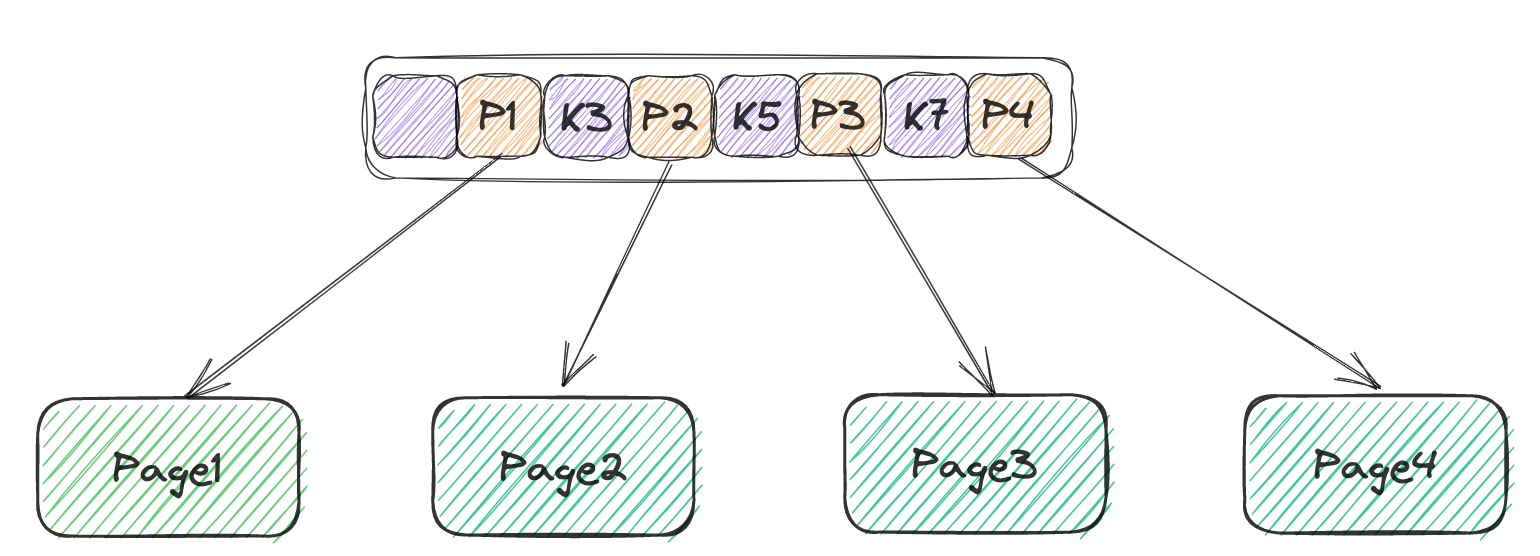
按照伪代码来严格实现，按照上图的划分方法进行封装，分别定义FindLeaf()，用于从根节点找到对应的叶子节点，在这过程当中需要在一个节点内部去搜索，因此分别定义一个LoopUp和KeyIndex：

KeyIndex：调用std::lower_bound去寻找第一个 >= 的值
LookUp：调用KeyIndex，根据返回的下表去判断是否获取到。

并且叶子节点和内部节点的搜索逻辑并不相同，因此需要分别定义。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE ::KeyIndex(const KeyType &key, const KeyComparator &comparator) const -> int {
 auto target = std::lower_bound(array_,array_ + GetSize(),key,
                                   [&comparator](const auto &pair,auto k) {
                                     return comparator(pair.first,k) < 0;
                                   }) ;
 return std::distance(array_,target);
}

INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE::LookUp(const KeyType &key, ValueType *valueType,
                                                                  const KeyComparator &keyComparator) const -> bool {
 int target_in_array = KeyIndex(key,keyComparator);
 if (target_in_array == GetSize() || keyComparator(array_[target_in_array].first,key) != 0) {
   return false;
 }
 *valueType = array_[target_in_array].second;
  return true;
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_INTERNAL_PAGE_TYPE::Lookup(const KeyType &key, const KeyComparator &comparator) const -> ValueType {
  // skip the empty key
  auto target = std::lower_bound(array_ + 1, array_ + GetSize(), key,
                                 [&comparator](const auto &pair, auto k) { return comparator(pair.first, k) < 0; });
  // larger than any key,return the last one
  if (target == array_ + GetSize()) {
    return ValueAt(GetSize() - 1);
  }
  // return the key == target_key
  if (comparator(target->first, key) == 0) {
    return target->second;
  }
  // return the key < target_key
  return std::prev(target)->second;
}

Insert

主要分为四个函数，分别为：

主体insert
当树为空时调用stratNewTree创建第一个节点
insert_in_leaf
insert_in_parent

Insert

insert本身并不实现什么具体逻辑，对StartNewTree和insert_in_leaf进行分类即可

1
2
3
4
5
6
7
8
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::Insert(const KeyType &key, const ValueType &value, Transaction *transaction) -> bool {
  if (IsEmpty()) {
     StartNewTree(key,value);
     return true;
  }
  return InsertIntoLeaf(key,value,transaction);
}

StartNewTree

创建一个全新的树，创建一个叶子节点将其作为根节点，并向其中插入一条数据

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::StartNewTree(const KeyType &key, const ValueType &val) -> void {
  auto page = buffer_pool_manager_->NewPage(&root_page_id_);
  if (page == nullptr) {
     throw Exception(ExceptionType::OUT_OF_MEMORY,"cannot allocate new page in StartNewPage");
  }
  auto *leaf = reinterpret_cast<LeafPage *>(page->GetData());
  leaf->Init(root_page_id_,INVALID_PAGE_ID,leaf_max_size_);
  leaf->Insert(key,val,comparator_);
  buffer_pool_manager_->UnpinPage(page->GetPageId(), true);
}

Insert封装在Leaf_page当中，找到一个合适的位置向其中插入，并且对于重复的key，拒绝插入。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
INDEX_TEMPLATE_ARGUMENTS
auto B_PLUS_TREE_LEAF_PAGE_TYPE::Insert(const KeyType &key, const ValueType &val,const KeyComparator &keyComparator) -> int {
  auto distance = KeyIndex(key,keyComparator);
  // larger than any key
  if (distance == GetSize()) {
   *(array_ + distance) = std::make_pair(key,val);
   IncreaseSize(1);
   return GetSize();
  }
  // duplicated key
  if (keyComparator(array_[distance].first,key) == 0) {
   return GetSize();
  }
  std::move_backward(array_ + distance,array_ + GetSize(),array_ +GetSize() + 1);
  *(array_ + distance) = std::make_pair(key,val);
  IncreaseSize(1);
  return GetSize();
}

Insert_in_leaf

对于不需要创建新树的情况，一律归类于向叶子节点当中插入数据

先通过GetValue当中实现的FindLeaf找到对应的叶子节点，之后直接向其中插入，如果叶子节点的大小没有发生变化，那么则证明为重复的key，直接返回即可。

如果大小发生变化但是没有超出最大值，无需进行分裂，也直接返回即可。

剩余的情况则是需要进行分裂。

叶子节点分裂

首先从buffer pool当中获取出一个新的Page用于承载分裂得来的新page
原本的节点保留minSize（maxSize / 2 )个数据，其他的全部拷贝至新的节点，最终的新节点当中的数据较多

当完成叶子节点的分裂之后，并将连接关系设置好之后，左右连接，parentId，之后再调用InsertIntoParent将右节点的第一个插入到父节点当中。

InsertIntoParent

首先需要说明的是调用InsertIntoParent的时机一定是在叶子节点当中插入引发了分裂，之后将新分裂出的右节点的第一个key尝试插入到父亲节点当中

对于伪代码当中的一条条来看：

如果N为根节点：则创建新的根节点，insert_in_parent由叶子节点开始调用，而此时N为根节点则证明已经递归到对根节点进行分裂，N‘即为N的新兄弟节点，因此需要创建一个新的根节点，以N，N‘为子节点，
对应以下的情况：K’ = 0003
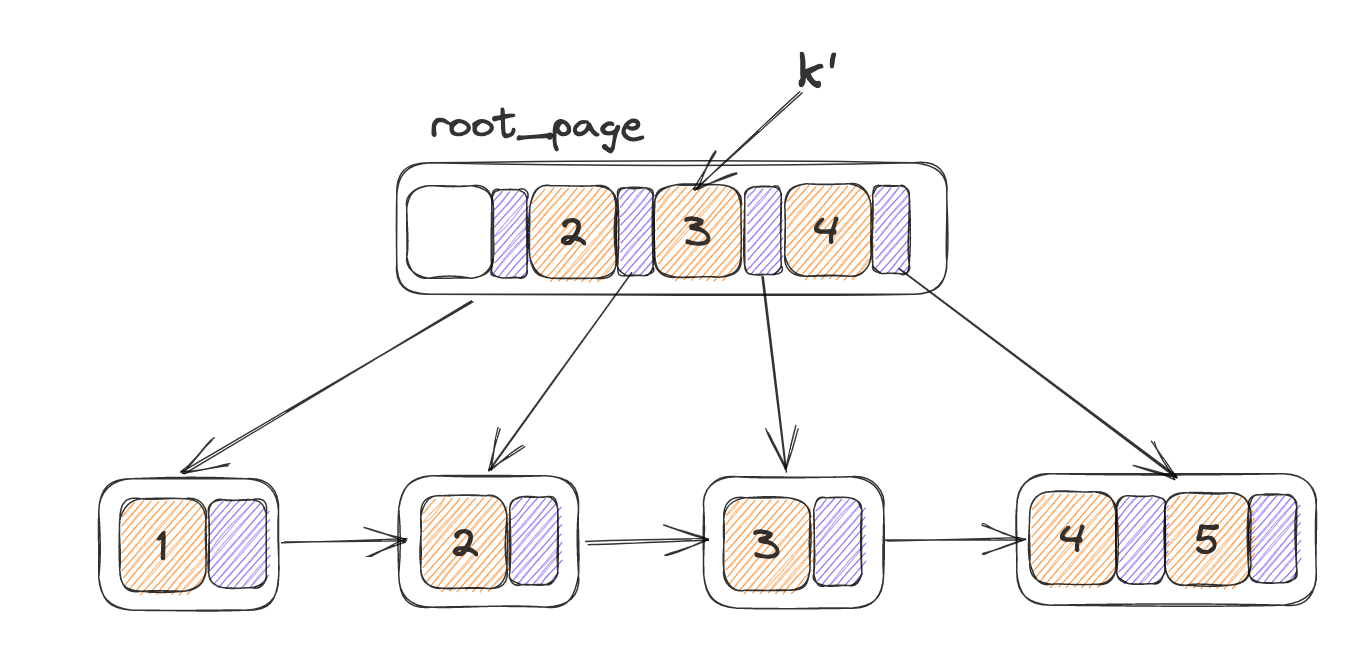
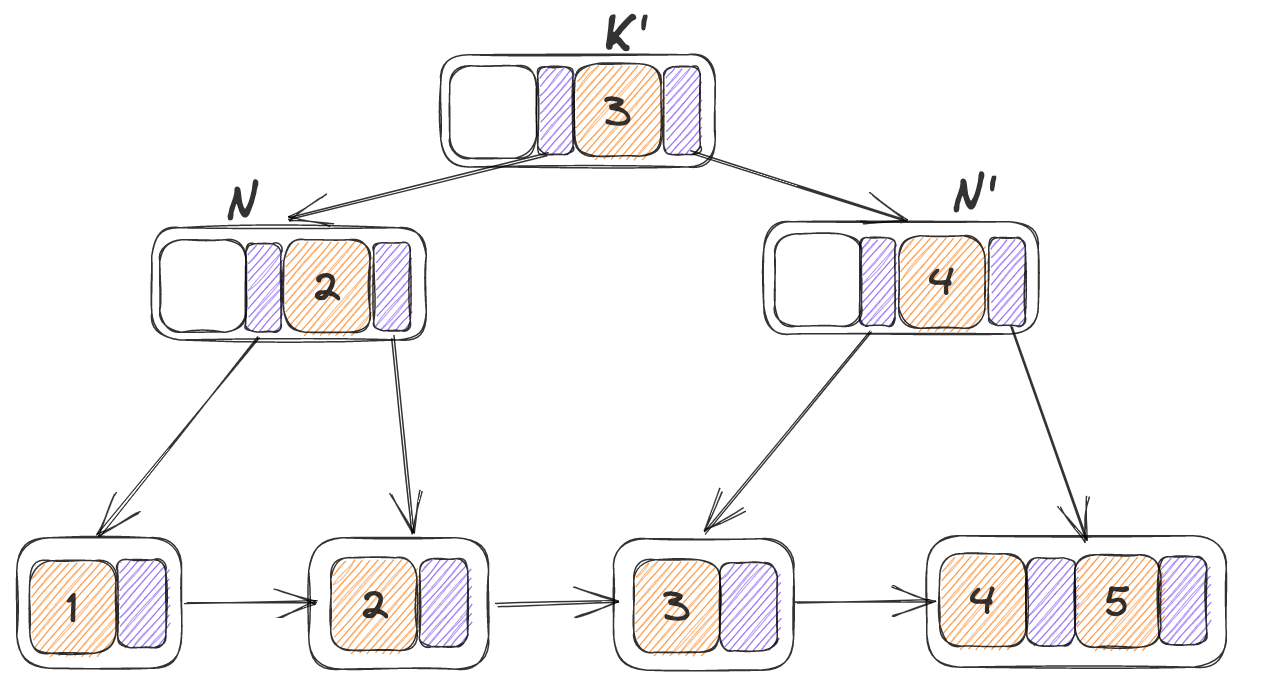
P有不到n个指针，还未满，在父节点当中直接插入并结束，没什么好说的
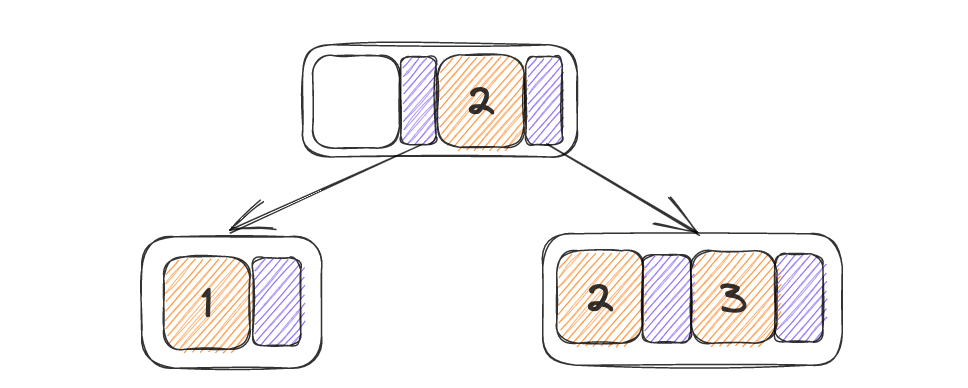
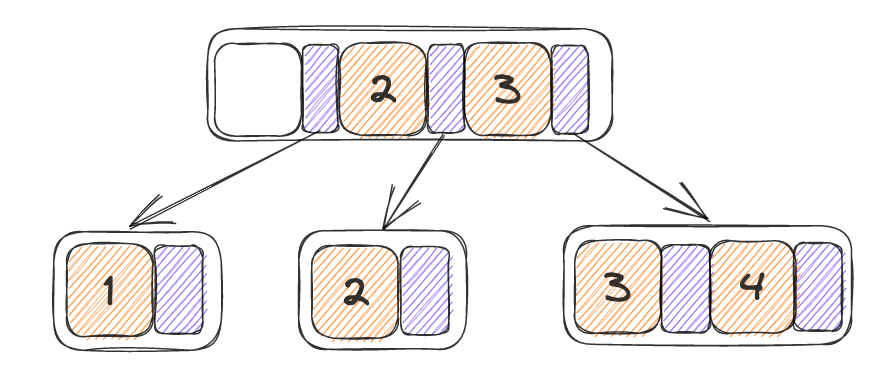
此时将6插入到父节点当中，父节点也无法容下，对父节点进行分裂，分裂完之后递归调用，在将5插入到上一级的父节点当中，此时可以容下5，因此不进行分裂，终止插入

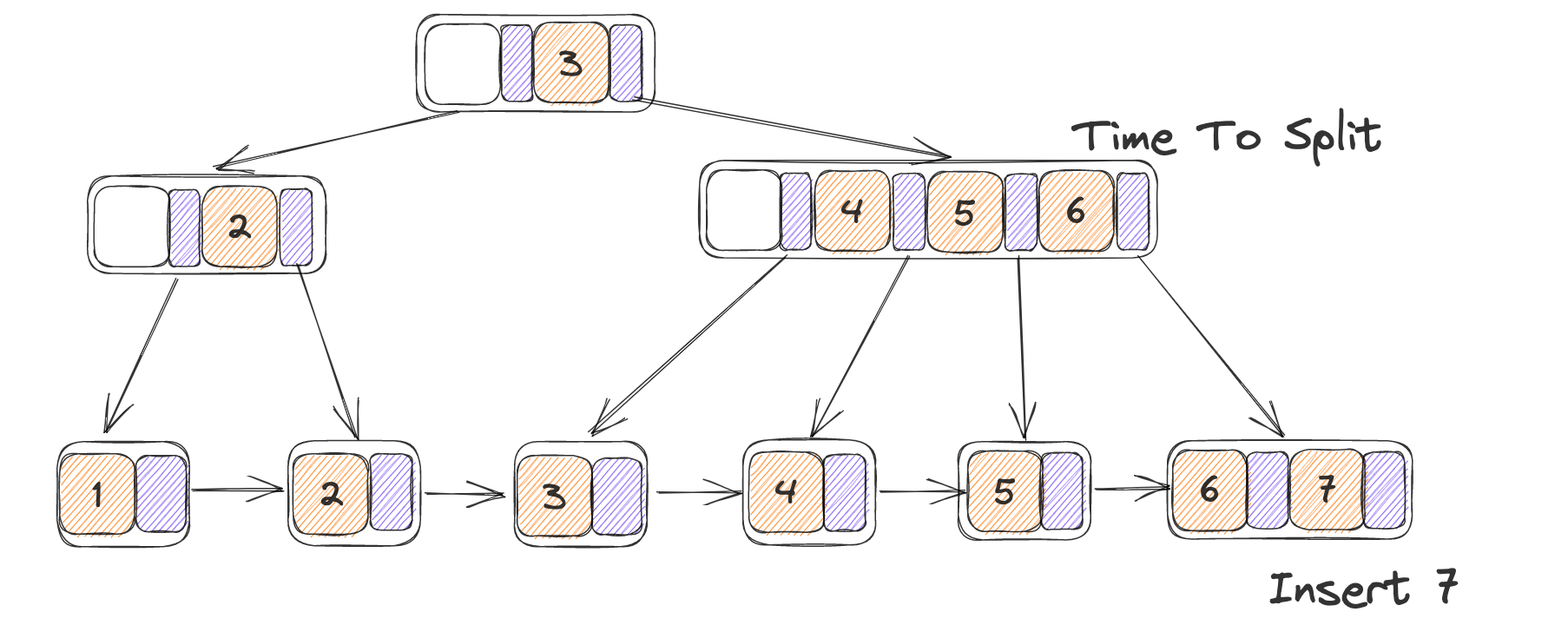
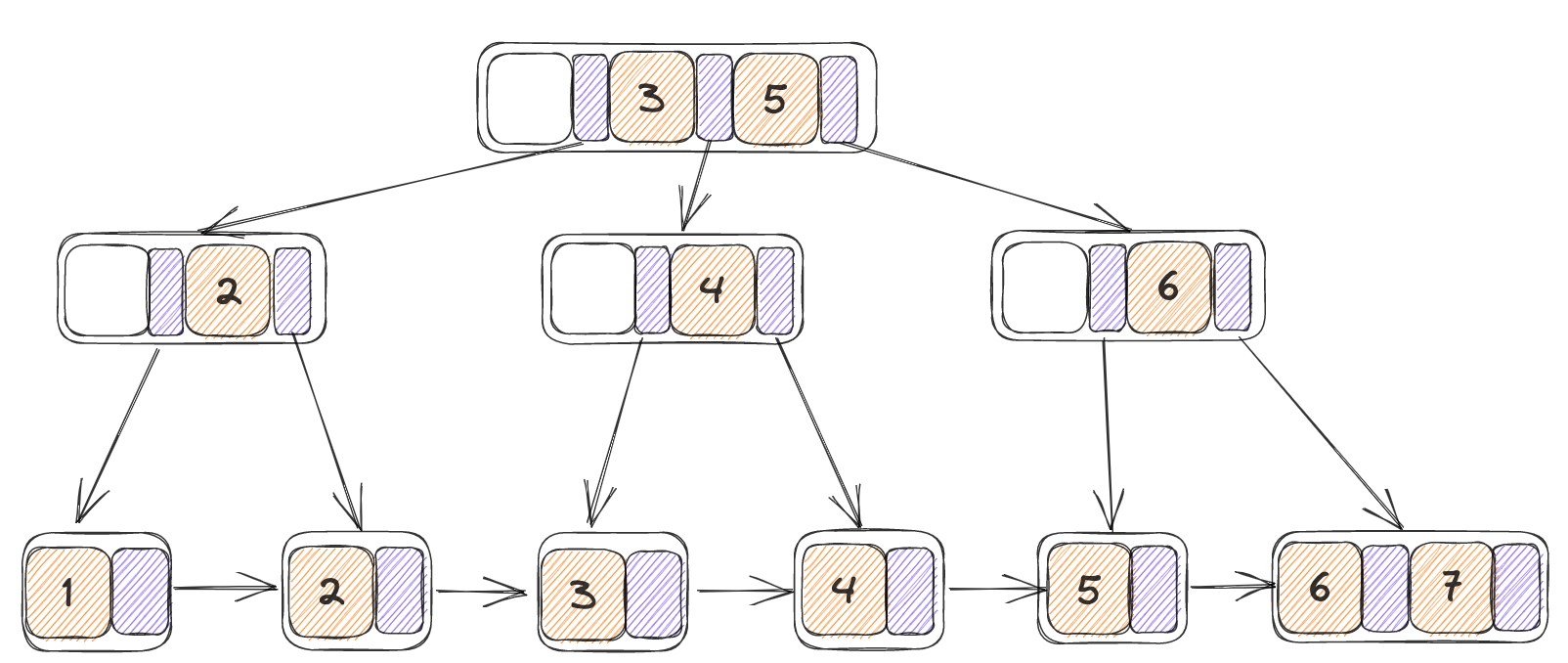
在整个插入过程当中一个比较重要的实现就是分裂，分裂的过程严格按照伪代码所给的进行实现，对于叶子节点和内部节点在分裂上的实现有所不同，因此定义一个Split来对叶子节点和内部节点的数据迁移和指针指向更改。

创建一块内存块用于存放所有的之前的所有数据和要新插入的K’ N’，
将旧节点的所有的数据都拷贝到其中，新插入的K‘N’也加入到其中。
完成节点的分裂，前一个节点保存min_size个节点，后一个节点保存其他的所有节点

按照伪代码描述，前一个节点应当保存(n+1)/2向上取整个节点，因此如果是基数个的话，那么前一个节点会比后一个节点多一个，但是个人认为这个是无所谓的，因为两种实现方法都能够达到平衡，在网上看到的两个B+树的演示动画也采用了两种不同的实现方式。

在分裂上的实现也不是很统一，由于对于叶子节点的分裂使用了先插入之后在判断的方式，因此直接分裂即可，对于内部节点需要在分裂前补上新的数据。伪代码当中的临时内存块其实不使用也可，直接在原节点上进行操作就行了。正确性上也可以得到保证(做完之后在网上看到了说直接插入会导致超出大小限制，但是我自己做下来按照直接插入的方式并没有出现什么问题)

1
2
3
4
5
6
  parent_node->InsertAfterNode(old_node->GetPageId(), key, new_node->GetPageId());
  auto parent_sibling_node = Split(parent_node);
  auto new_key = parent_sibling_node->KeyAt(0);
  InsertIntoParent(parent_node, new_key, parent_sibling_node);
  buffer_pool_manager_->UnpinPage(parent_page->GetPageId(), true);
  buffer_pool_manager_->UnpinPage(parent_sibling_node->GetPageId(), true);

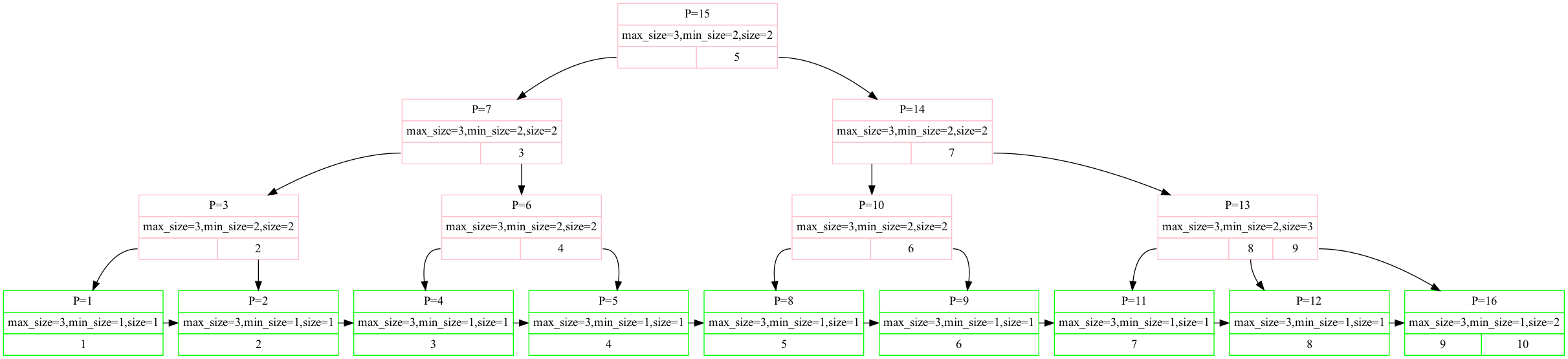
Delete

相对于插入来说，删除的逻辑就复杂的多,函数拆分方式如上，还是一条条的看。

下面的例子全以MaxDegree = 4，MaxSize = 4,MinSize = 2来进行讨论

最开始通过FindLeaf() 找到Key所在的leaf_page，之后调用delete_entry进行删除，不过由于后续涉及到递归调用，因此可以把从leaf_page中删除的逻辑移到delete_entry外面

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::Remove(const KeyType &key, Transaction *transaction) {
  if (IsEmpty()) {
    return;
  }
  auto leaf_page = FindLeaf(key, transaction);
  auto *node = reinterpret_cast<LeafPage *>(leaf_page->GetData());

  if (node->IsLeafPage()) {
    auto before_size = node->GetSize();
    auto size = node->Delete(key, comparator_);
    if (before_size == size) {
      // cannot find the key;
      return;
    }
  }
  DeleteEntry(node, key);
}

AdjustRoot

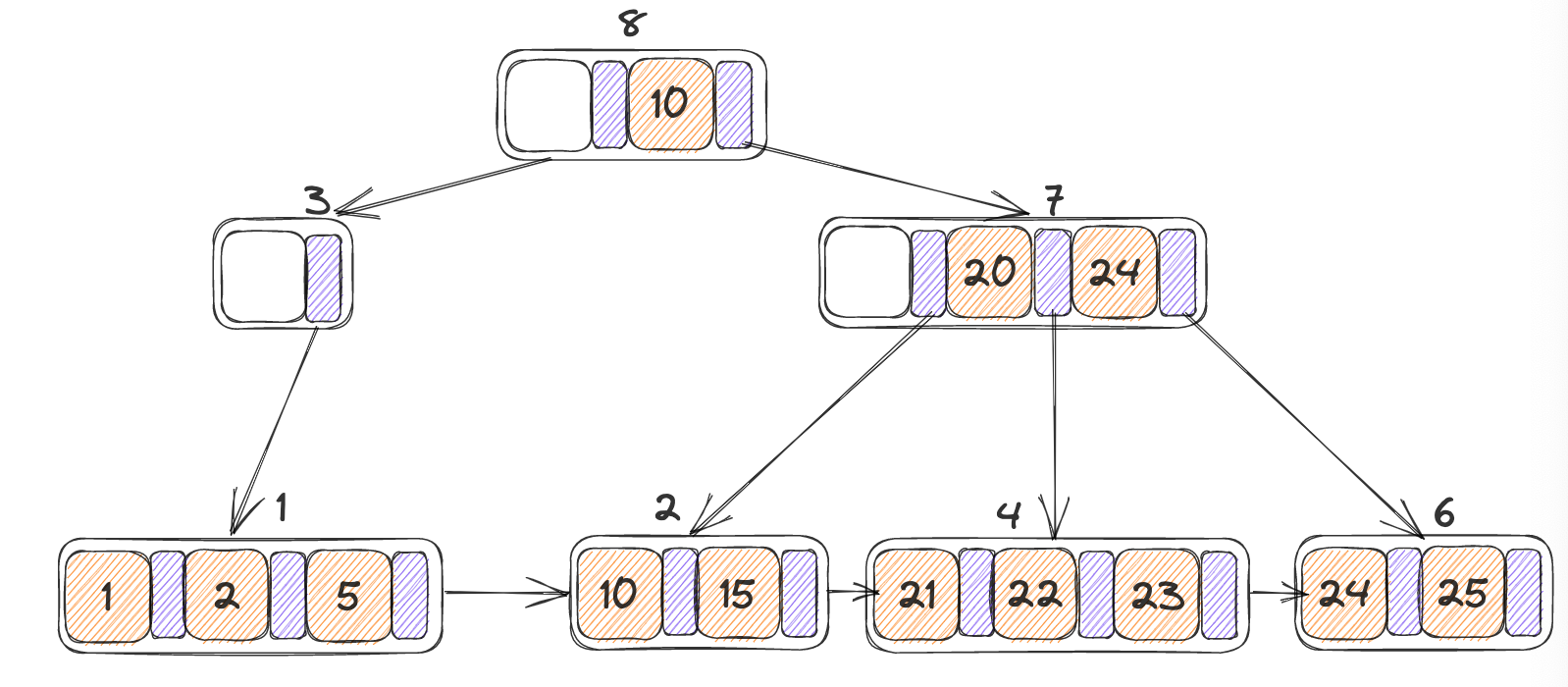
一棵树的初始状态如下，此时如果需要从中删除掉Key = 3，叶子节点当中的key不够，并且能够与左节点合并而不达到MaxSize，因此进行合并
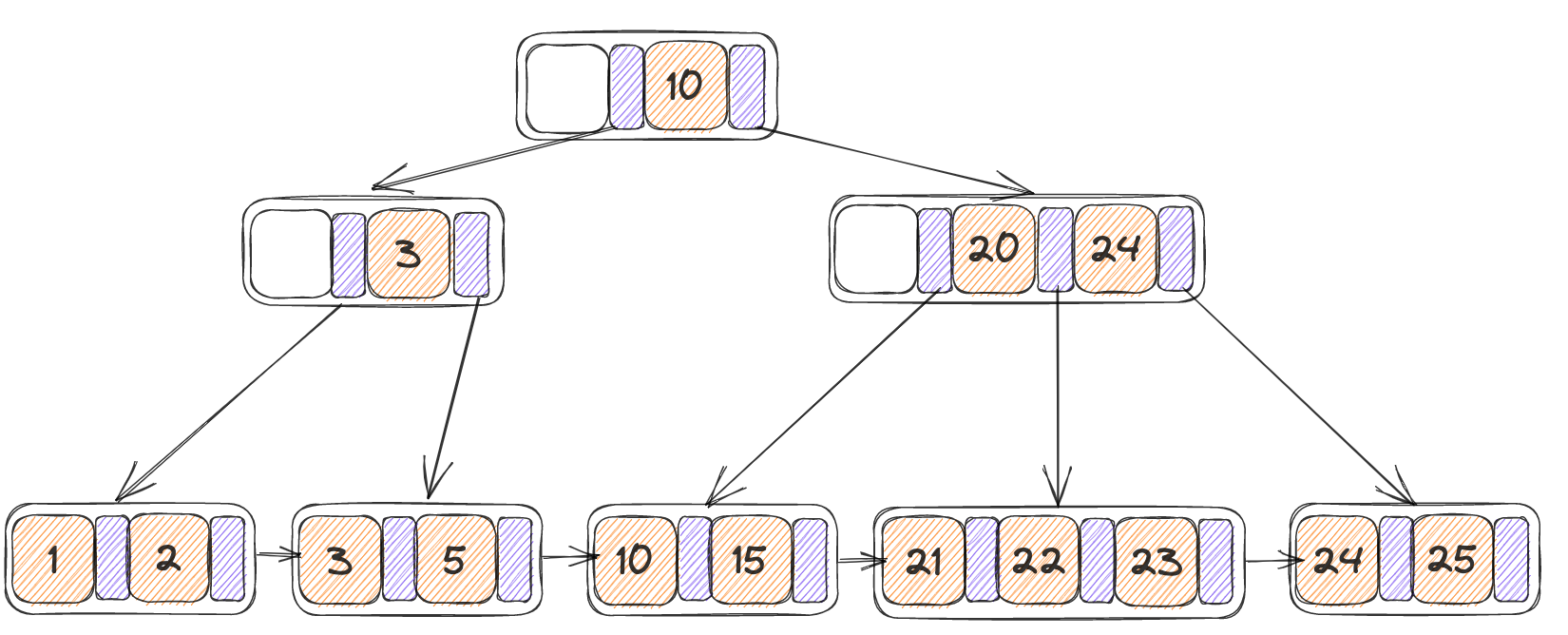
合并结果如下，此时的3号节点当中只有一个指针，小于min_size，同样的与右节点合并之后不会超过max_size，因此合并
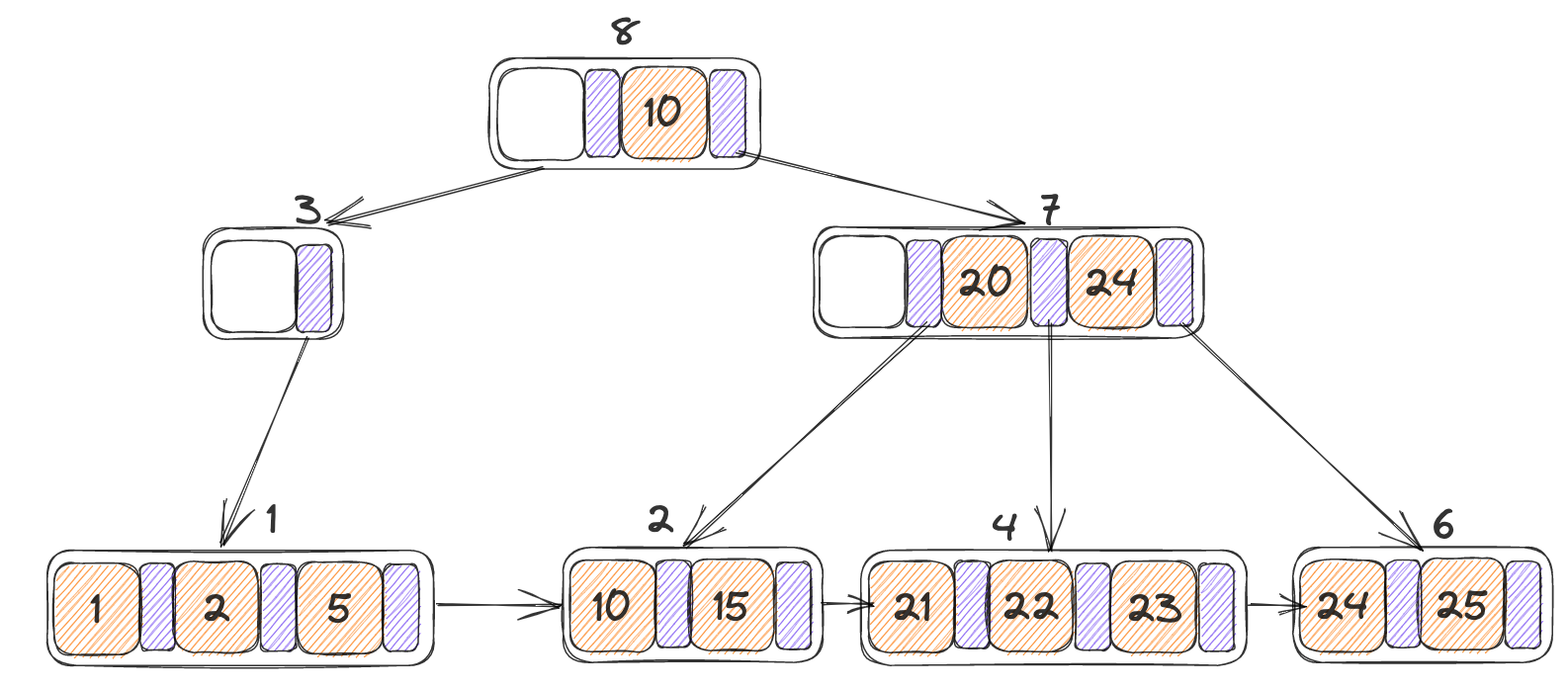
合并的结果如下，并且合并之后会在递归调用一次delete_entry，此时传入的节点即为parent(N)，找到了根节点，并且此时的根节点只有一个孩子，达到了AdjustRoot的条件：
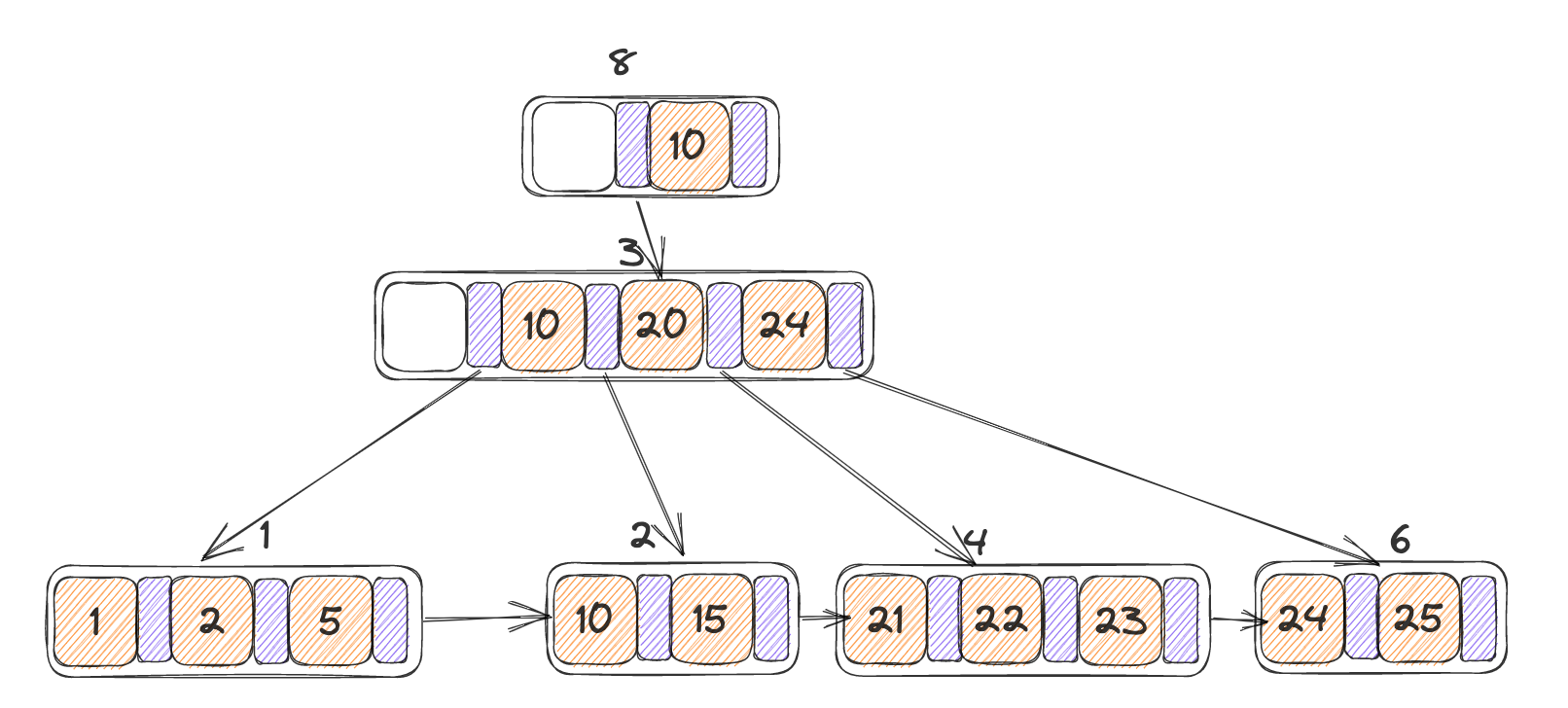
最终AdjustRoot的结果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::AdjustRoot(BPlusTreePage *old_root_node) -> bool {
  if (!old_root_node->IsLeafPage() && old_root_node->GetSize() == 1) {
    auto *root_node = reinterpret_cast<InternalPage *>(old_root_node);
    auto only_child_page = buffer_pool_manager_->FetchPage(root_node->ValueAt(0));
    auto only_child_node = reinterpret_cast<BPlusTreePage *>(only_child_page);
    only_child_node->SetParentPageId(INVALID_PAGE_ID);
    root_page_id_ = only_child_node->GetPageId();
    UpdateRootPageId(0);
    buffer_pool_manager_->DeletePage(old_root_node->GetPageId());
    return true;
  }
  return false;
}

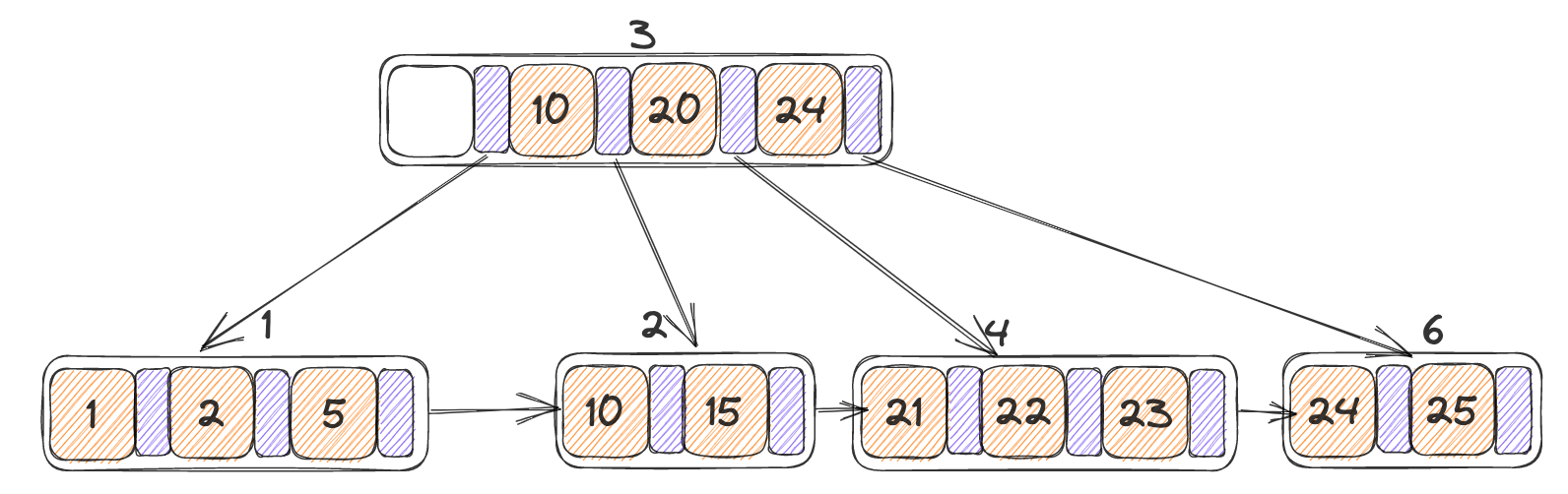
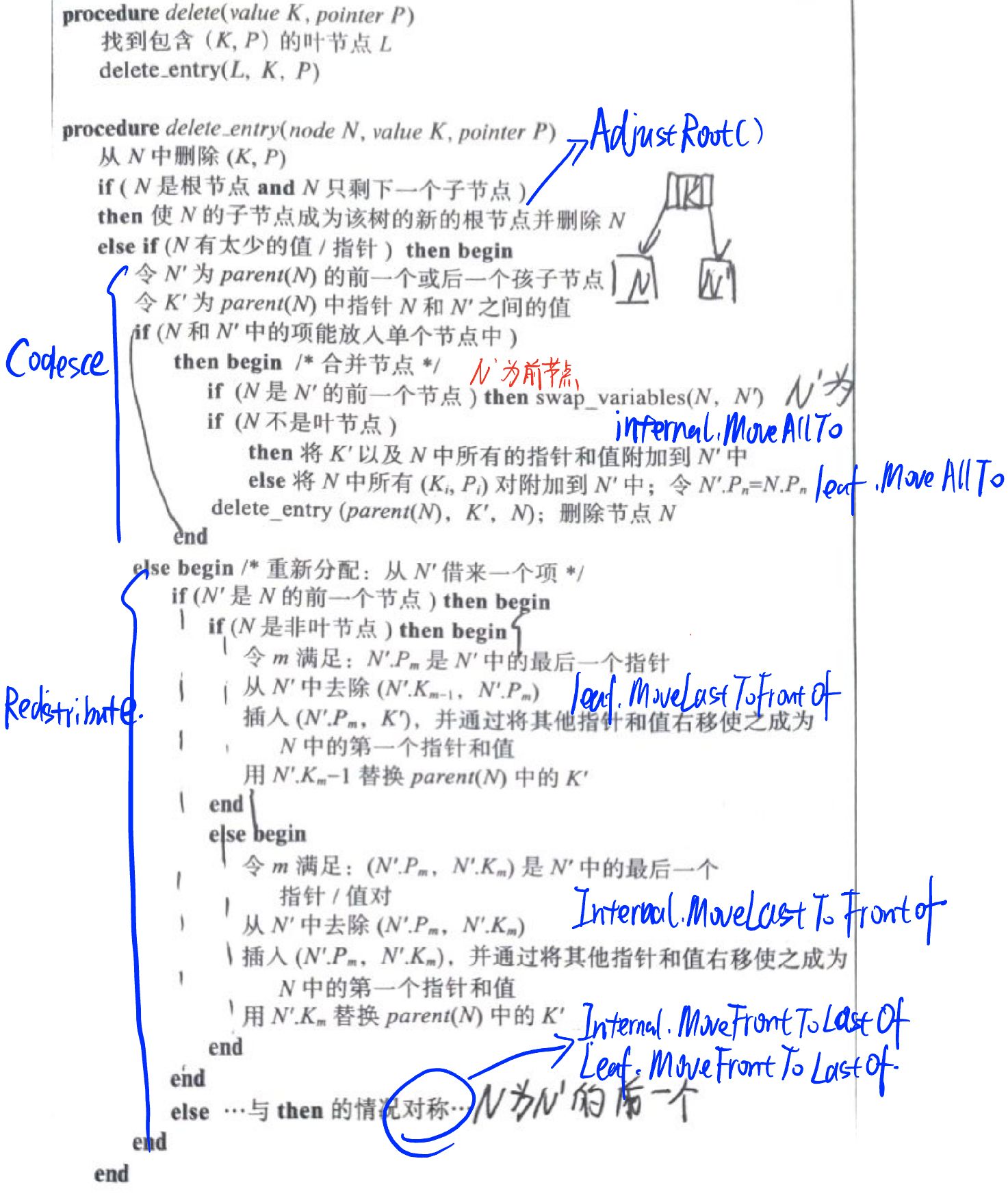
Coalesce：

当两个节点合并之后仍小于MaxSize时，对两个节点进行合并，在逻辑上同样需要分为对叶子节点进行操作和对内部节点进行操作，由于在上述AdjustRoot的例子当中已经涉及到了根节点的合并和叶子节点的合并，因此就还用上面的例子

叶子节点的合并

初始树：
1. 将3进行删除，之后发现其左节点与之合并之后仍小于max_size，此时的N为自身，N’为其左节点，K’为3，
2. 执行合并，将右叶子节点当中的所有KV移动到左节点当中
3. 递归调用delete_entry，在父亲节点当中尝试删除掉K’(3)
4. 递归完之后清除掉N
最终结果如下，而当前的3号page当中只有一个指针，因此是不稳定的，并且大小允许合并，执行内部节点的合并

内部节点的合并

初始树，已经删除掉K之后
1. N为自身节点，N’为其右节点，K’按照定义即为10，将N作为最终合并后的存储节点
2. 因此先将K’添加到N当中，之后在将N’当中所有的KV添加到其中（不包括第一个空的K）
最终结果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
auto BPlusTree<KeyType, ValueType, KeyComparator>::Coalesce(
    N *left_node, N *right_node, BPlusTreeInternalPage<KeyType, page_id_t, KeyComparator> *parent, int index) -> bool {
  auto middle_key = parent->KeyAt(index);
  if (!right_node->IsLeafPage()) {
    auto *internal_node = reinterpret_cast<InternalPage *>(right_node);
    auto *internal_left_node = reinterpret_cast<InternalPage *>(left_node);
    internal_node->MoveAllTo(internal_left_node, middle_key, buffer_pool_manager_);
  } else {
    auto *leaf_node = reinterpret_cast<LeafPage *>(right_node);
    auto *leaf_left_node = reinterpret_cast<LeafPage *>(left_node);
    leaf_node->MoveAllTo(leaf_left_node);
    parent->Remove(index);
  }
  DeleteEntry(parent, middle_key);
  buffer_pool_manager_->DeletePage(right_node->GetPageId());
  return true;
}

Redistribute

同样需要分为叶子节点和内部节点来进行讨论，内部节点由于0号位Key为空，因此无法像合并那样直接交换顺序即可，而是需要实现一个逻辑上一样的对称操作。

叶子节点重分配

初始树：
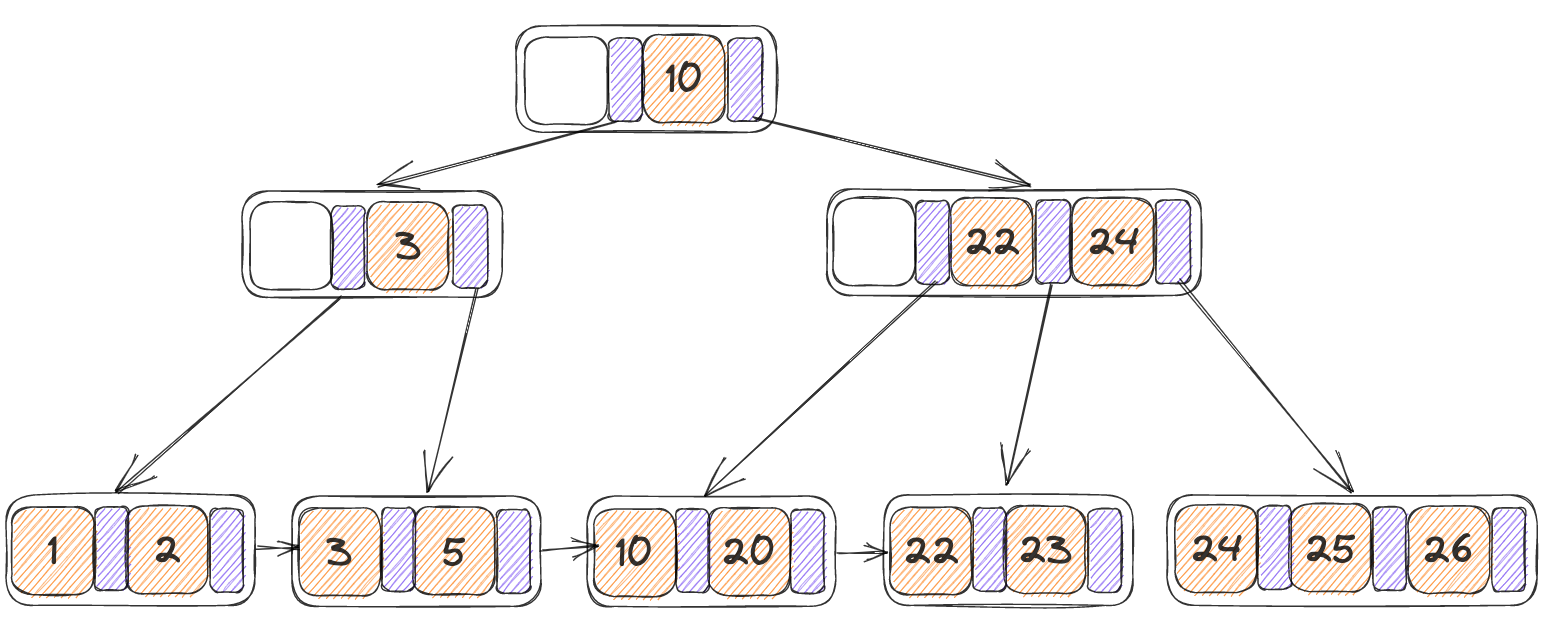
此时尝试从中删除掉23，此时该叶子节点当中就只剩下一个KV，小于min_size，并且无法和右节点进行合并，因此需要进行redistribute(代码逻辑中先判断是否能进行重分配，如果不能在后续判断合并，重分配本身不涉及到递归调用，因此对整个B+树的调整范围小，开销较小)
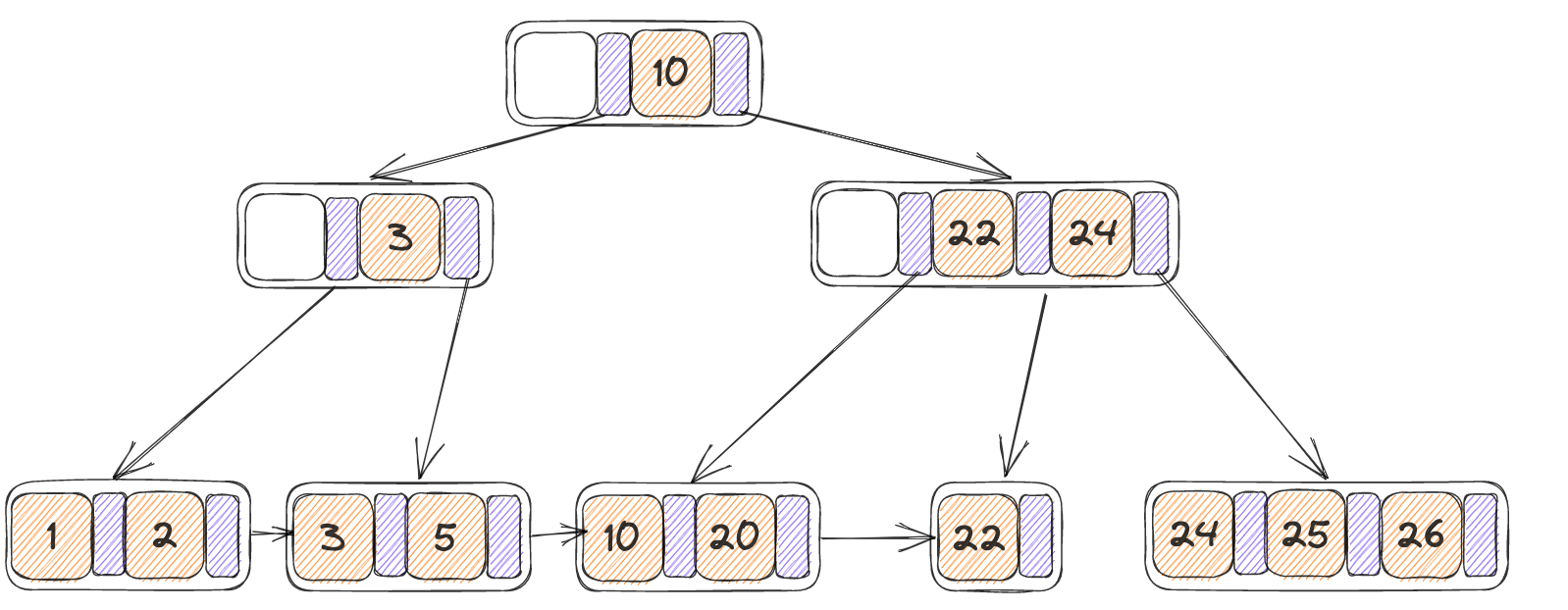
自身为N，右节点为N‘，将N‘当中的第一个KV移动至N的末尾，并且将parent当中N,N’中间的key替换为移动之后的N‘当中的第一个K（25），最终结果如下：

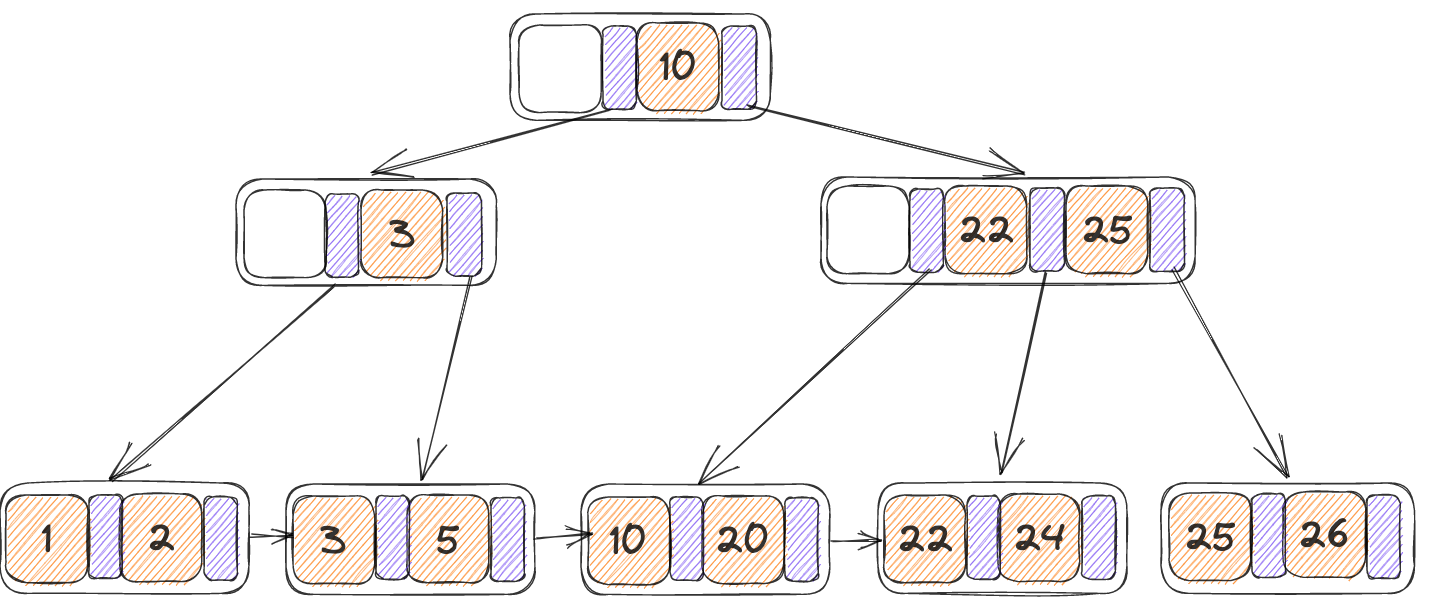
叶子节点的为完全对称的，因此只需要完全对称的实现即可，将第一个改为最后一个，逻辑上完全一致。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
  if (node->IsLeafPage()) {
    auto *leaf_node = reinterpret_cast<LeafPage *>(node);
    auto *leaf_neighbor_node = reinterpret_cast<LeafPage *>(node);
    if (from_prev) {
      leaf_neighbor_node->MoveLastToFrontOf(leaf_node);
      parent->SetKeyAt(index, leaf_node->KeyAt(0));
    } else {
      leaf_neighbor_node->MoveFrontToLastOf(leaf_node);
      parent->SetKeyAt(index, leaf_neighbor_node->KeyAt(0));
    }
  }

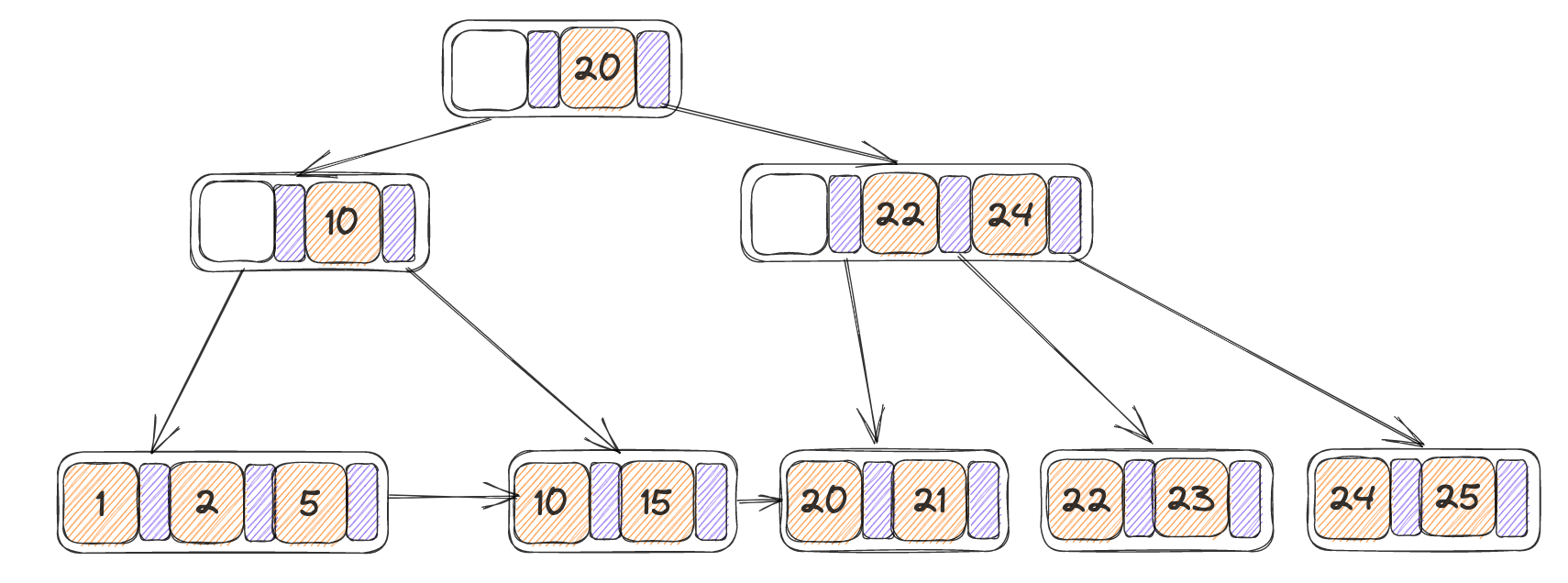
内部节点重分配

初始树和从中删除掉3之后的状态分别如下：
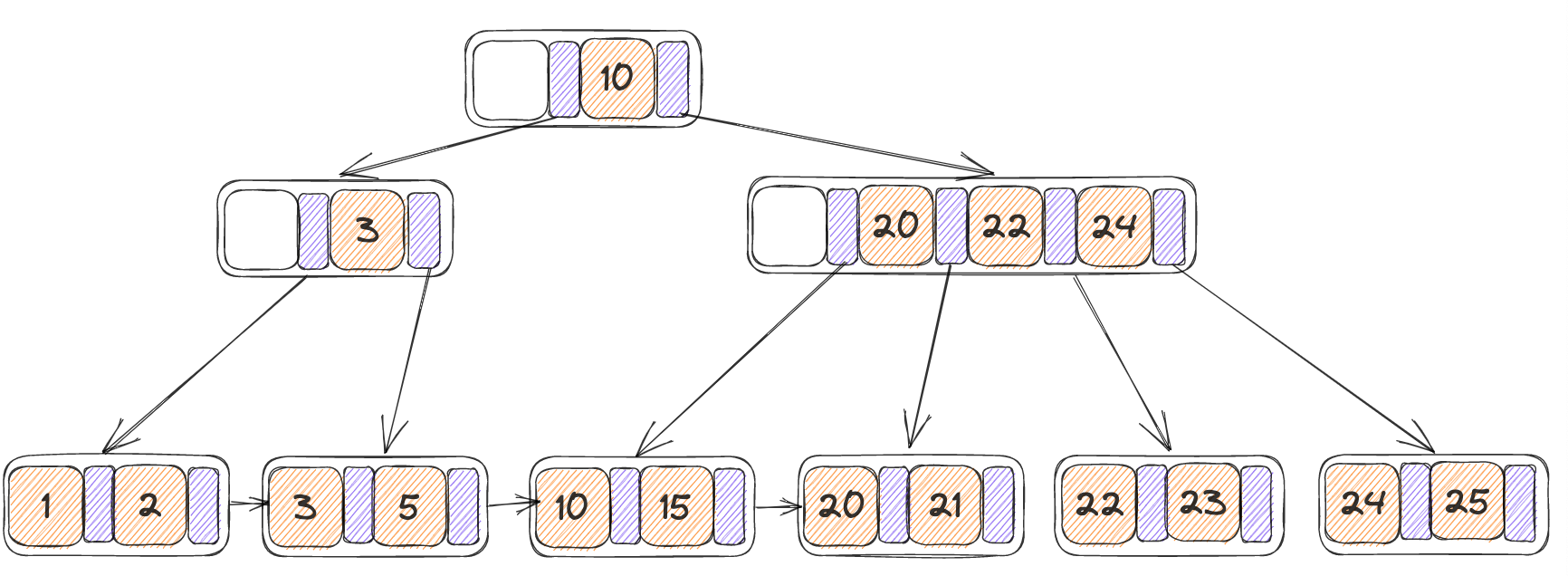
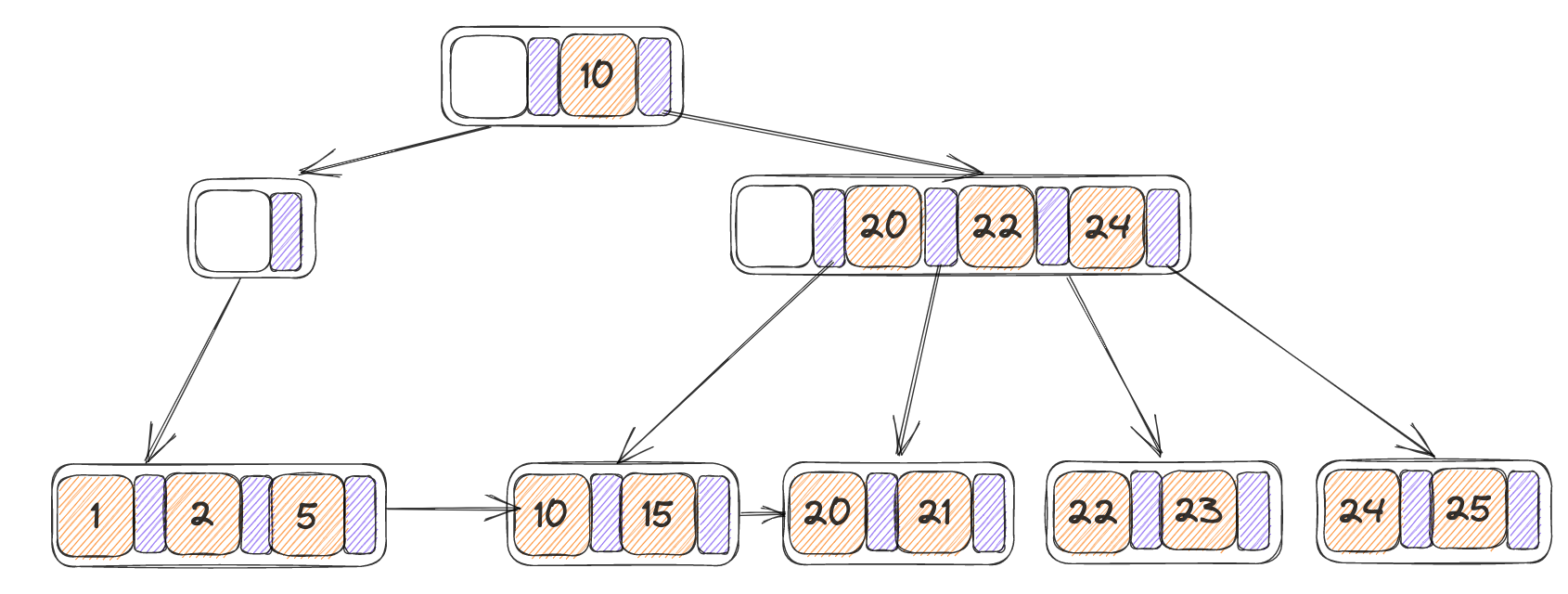
1. 此时左侧只剩下一个指针，并且合并会大于max_size，因此进行重分配，N为自身，N’为其右节点
2. 找到N’当中的第一个KV，记为(K1,V1)，将其添加到N的末尾
3. 找到在parent(N)当中的N与N’指针之间的K’，将N的最后一个K设置为K’，并将parent(N)当中的K’设置为K1
最终结果如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
    auto *internal_node = reinterpret_cast<InternalPage *>(node);
    auto *internal_neighbor_node = reinterpret_cast<InternalPage *>(neighbor_node);
    if (from_prev) {
      internal_neighbor_node->MoveLastToFrontOf(internal_node, parent->KeyAt(index), buffer_pool_manager_);
      parent->SetKeyAt(index, internal_node->KeyAt(0));
    } else {
      auto new_parent_key = internal_neighbor_node->KeyAt(1);
      internal_neighbor_node->MoveFrontToLastOf(internal_node, parent->KeyAt(index + 1), buffer_pool_manager_);
      parent->SetKeyAt(index + 1, new_parent_key);
    }

对于内部节点的重分配，存在那么一点不对称的情况：

即上述例子为在左节点当中检测到需要进行合并，由于第一个空key的存在，K’的位置应当为index + 1,(index为N在parent当中的位置)，而如果是从右侧检测到需要进行重分配，K’即为index
右侧向左侧添加时应当添加index = 1的KV，跳过空Key，左侧向右侧添加时，同样添加到一号位置

实现的时候注意一下即可。

Lab2#

Task1#

节点实现#

节点大小#

实现方式#

Task2#

GetValue#

Insert#

Insert#

StartNewTree#

Insert_in_leaf#

InsertIntoParent#

Delete#

AdjustRoot#

Coalesce：#

Redistribute#

Lab2

Task1

节点实现

节点大小

实现方式

Task2

GetValue

Insert

Insert

StartNewTree

Insert_in_leaf

InsertIntoParent

Delete

AdjustRoot

Coalesce：

Redistribute