checkpoint2

Task3

在支持并发前没什么好说的，一个简单的迭代器。根据begin的条件找到一个起始页，之后在该页内遍历即可，当遍历完该页之后，根据nextPageId找到下一页继续遍历即可。

Unpin

最初通过FindLeaf找到一个page，对其进行了fetch，此时是对其pin住了的，当遍历完该page之后应该对该page进行unpin，当迭代器析构时，应当对当前页unpin。

并发这里先不说，留在Task4当中进行实现。

Task4

个人感觉相比于checkpoint1来说，其实并不难，在细节的处理上并没有checkpoint1当中复杂，尤其是delete操作，个人在delete上花费了大量时间进行理解和debug，并且在checkpoint1的测试数据并不完善，根据群友扒下来或者自己复刻的结果来看，对于delete的测试只有两个，并且一个单元测试当中只插入了五条数据进行测试，测试强度很低，这也导致很多问题在checkpoint1当中并没有暴露出来，最终混在了checkpoint2当中。

并发

对B+树支持并发，使用所谓的螃蟹锁，只有在子节点安全的情况下才能够释放掉位于父节点上的锁，对于安全的情况根据操作而定：

Search：从父节点上获取到R锁，之后遍历子节点，只要在子节点上获取到锁之后，就可以认为当前已经安全，之后便可以释放掉位于父节点上的锁。
Insert：从根节点开始，尝试在子节点上获取W锁，一旦在孩子节点上获取锁成功，那么就检查是否安全，对于插入情况而言，如果插入后不产生分裂则视为安全，如果安全，那么就是释放所有祖先的锁
Delete：从根节点开始，尝试在子节点上获取W锁，一旦锁定，检查是否安全，对于删除情况而言，为至少半满（对于根节点需要按照不同的标准的检查），一旦孩子节点安全，释放所有祖先的锁。

在并发的实现上，主要涉及两点,一个是通过Latch Crabbing在FindLeaf的途中一遍获取一遍释放锁，保证并发安全的同时提高并发度（此外还有delete时对兄弟节点加锁）。另一个则是在合适的位置释放掉和当前事务相关的锁。

锁的形式

首先，所有的Page都是通过buffer pool进行获取的，只有通过buffer pool获取到了Page之后，才可以进行后续的操作，而从buffer_pool当中获取到的最初即为原始的Page，而不是对内存重新解释而来的BPlusTreePage，而在Page的头文件当中也给出了读写的latch，因此，对于单个Page的上锁，使用Page当中定义的ReaderWriterLatch即可。

root_page

root_page同样是通过buffer_pool来获取并之后进行上锁的，正常情况下不需要进行额外的操作，但是如果一颗树根本不存在，那么这时就没有办法去获取root_page并且进行上锁，因为无法对一个不存在的page进行上锁，个人感觉这里的处理方式就有点类似于幻读的间隙锁，由于无法对一个不存在的page进行上锁，那么就对其间隙进行上锁，这里的间隙指的就是树的开头，在root_page的上面虚构一个节点，在获取root_page之前先获取该节点，当能够对root_page上锁之后就释放掉该锁。

transaction

对Page访问的基本单位为transaction，因此transaction需要对于自己当前获取的锁进行保存和管理，这在transaction当中已经给了定义，通过GetPageSet()即可获取到管理当前相关page的队列。

并且获取锁时为按照自上向下的顺序来获取锁，释放时同样按照自顶向下的顺序进行，并且由于顶上的竞争较为激烈，提前释放也有利于提高并发度。

该队列只用于管理内部节点上的锁，对于进行插入或删除的叶子节点不进行管理，单独释放叶子节点上的锁。

Latch Crabbing

所谓的螃蟹锁，通过提前释放锁的形式来增加并发度。大致含义上为从根节点开始，先获取一个节点的锁，之后再尝试获取其子节点的锁，当获取到了子节点的锁之后，如果此次操作对于子节点来说是安全的，那么就可以释放掉该节点上的锁。就像螃蟹那样，放下一只脚往前走（获取子节点的锁），在抬起另一只脚（释放当前节点上的锁）

对于是否安全需要根据读写的形式进行判断：

对于读操作，并不存在什么安全不安全的问题，只要能够获取到子节点的锁，那么就是安全的，此时就可以释放掉当前节点上的锁
对于插入操作：只有当执行到最后一步找到叶子节点之后才能够知道是否会引发分裂，以及分裂是否会向上作用。但是，在遍历到内部节点时，可以知道是，如果发生了分裂，当前节点是否会发生分裂。即在遍历到过程中，获取到子节点的锁之后，假设子节点发生了分裂，来判断子节点的分裂导致的InsertIntoParent是否会引发自身的分裂，如果不会，那么就可以释放掉自身的锁，否则继续持有。
对于删除操作：逻辑上和插入操作差不多，只不过是否安全的判断标准为是否引起收缩。

对于Latch Crabbing，其虽然无法保证在持续占有锁的时候，后续一定会用到该锁，即对于一个五阶B+树，当前的内部节点，已经含有了4个key，5个value，此时根据条件应当继续持有锁，但是最终的子节点当中只有一对kv，因此不会发生分裂，此时的持有锁就属于白白持有了，后续不会用到，虽然这在情况对于并发度有一定影响，但是可以保证所有情况下的正确性。

在实现上主要是在FindLeaf当中，首先，FindLeaf调用时是从根节点进行搜索的，因此首先需要获取到root_page上的锁，并且判断是否安全，从而释放掉root上的锁。

之后，则循环找到叶子节点，反复的获取子节点的锁，然后判断自身是否安全，从而选择是否释放锁。

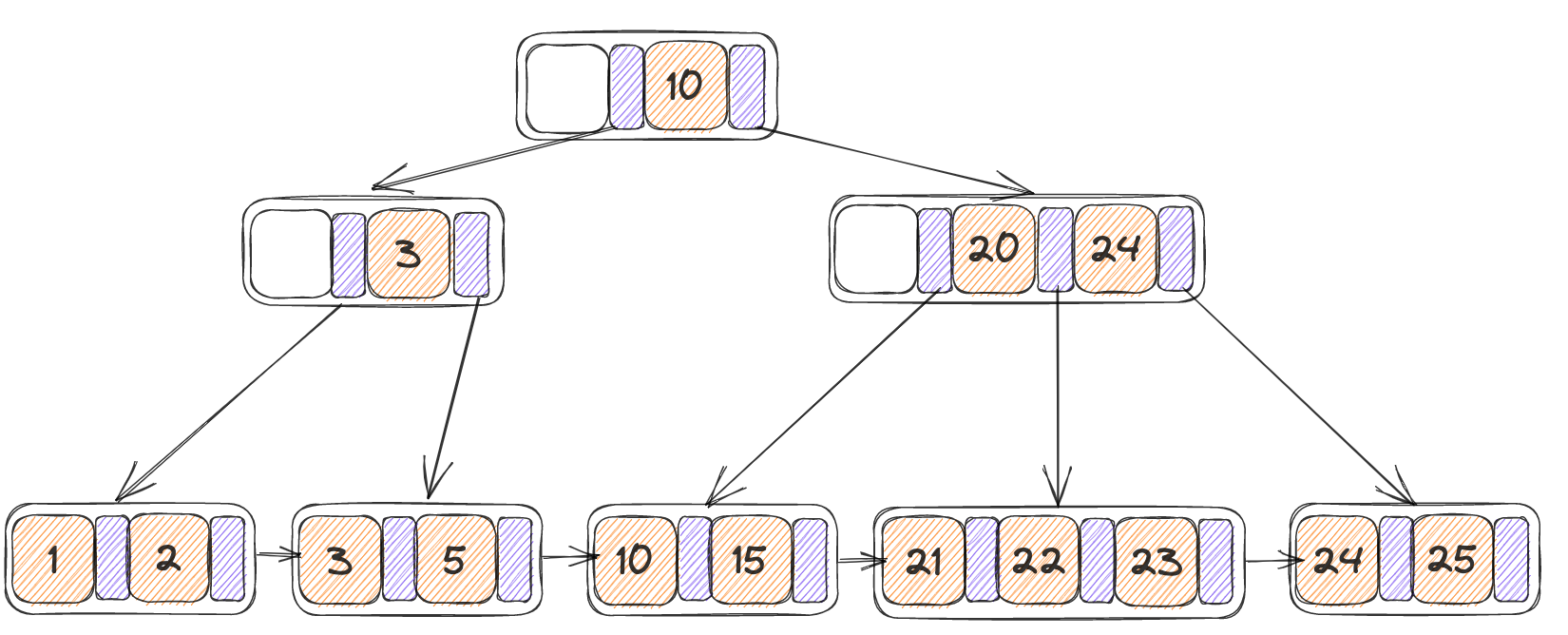
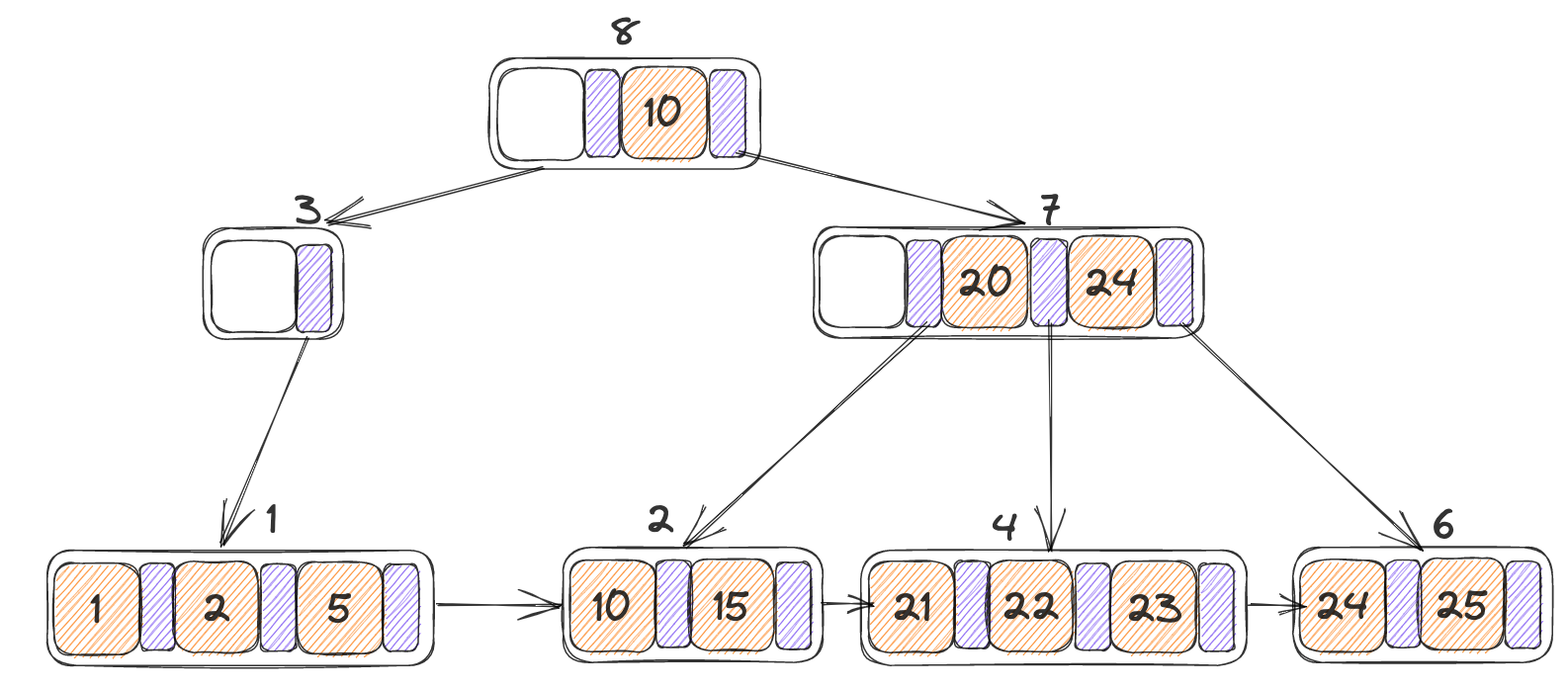
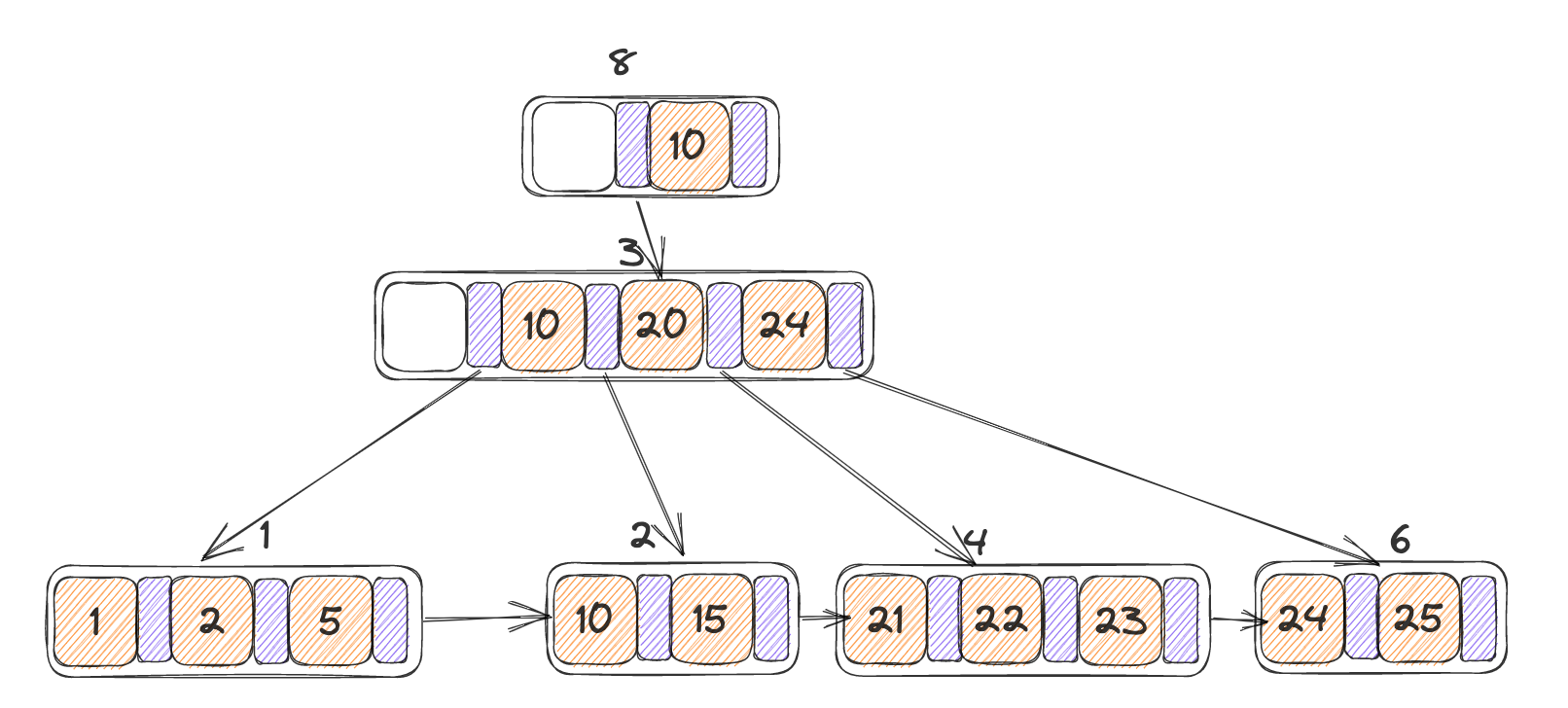
这里主要需要注意一下删除操作的根节点，在Lab的页面上也给出了相关提示，根据定义，一个根节点最少有两个子节点，反过来的意思就是如果只有两个字节点的情况下，如果一个节点被删除掉，那么就可能触发AdjustRoot()，因此对于删除情况下的根节点的安全条件是子节点数大于3。

下图中如果删除节点3则会引发AdjustRoot()，因此不能释放锁。

锁的释放

无论是GetValue,Insert还是Remove，都需要依赖FindLeaf来找到对应的leaf_page，之后进行具体的操作。因此调用完FindLeaf找到leaf_page之后，当前的事务是持有者该leaf_page的锁的，如果不安全的话，还有可能持有祖先节点的锁。因此就需要在合适的时机释放掉leaf_page上的锁和所有祖先节点上的锁，大致逻辑就是在Search、Insert、Remove三个函数FindLeaf之后、返回之前找一个合理的位置进行一次锁的释放，释放掉叶子节点和

Search

对于读操作，实现起来较为简单，直接使用螃蟹锁即可，其不存在什么不安全的情况，因此只需要当获取到孩子节点的锁之后，就可以释放掉父亲节点上的锁。锁的类型为读锁。

因此只需要在GetValue返回前释放掉叶子节点上的锁即可。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::GetValue(const KeyType &key, std::vector<ValueType> *result, Transaction *transaction) -> bool {
  root_page_latch_.RLock();
  auto leaf_page = FindLeaf(key, Operation::SEARCH, transaction);
  auto *node = reinterpret_cast<LeafPage *>(leaf_page->GetData());
  ValueType v;
  auto is_existed = node->LookUp(key, &v, comparator_);
  buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false);
  leaf_page->RUnlatch();
  if (is_existed) {
    result->push_back(v);
    return true;
  }
  return false;
}

Insert

Insert则涉及到一个安全问题，因此按照latch crabbing的策略，每次获取到锁之后都要尝试判断一次是否安全，即判断在子节点当中插入之后是否会产生分裂，如果不会产生，那么就可以释放掉之前所有的锁：

对于内部节点，则判断size < maxSize
对于叶子节点，则判断size < maxSize - 1

在释放锁时需要释放当前节点以及当前节点所有的祖先节点的锁，即将transaction的page队列当中的所有的page上的锁全部释放，并且注意根节点的处理。

相关函数：

Insert：入口函数：锁住root_page_latch
StartNewTree：创建一个新的root_page并向其中添加数据，已经在Insert当中上锁，无需操作
InsertIntoLeaf：已经存在一棵树，找到叶子节点并插入数据，调用FindLeaf找到叶子节点，此时还未释放叶子节点上的W锁，并且可能持有祖先节点上的锁，如果不涉及到分裂，W锁的释放和UnpinPage一同进行，在返回前释放。
InsertIntoParent：最初为LeafPage发生分裂而调用，调用时旧节点上的锁并未释放，整个过程中保持持有锁即可，等到返回之后再释放锁。

综上，对于Insert操作只需要才StartNewTree和InsertIntoLeaf执行结束后释放锁即可，当时为了将资源释放的逻辑进行统一，将释放锁的操作和InsertIntoLeaf当中和Unpin放在了一起。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::InsertIntoLeaf(const KeyType &key, const ValueType &val, Transaction *transaction) -> bool {
  auto leaf_page = FindLeaf(key, Operation::INSERT, transaction);
  // hold the latch of leaf_page and unsafe internal page
  auto *node = reinterpret_cast<LeafPage *>(leaf_page->GetData());
  auto size = node->GetSize();
  auto new_size = node->Insert(key, val, comparator_);
  if (size == new_size) {
    // duplicate key
    leaf_page->WUnlatch();
    ReleaseLatchFromQueue(transaction);
    buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false);
    return false;
  }
  if (new_size < leaf_max_size_) {
    leaf_page->WUnlatch();
    ReleaseLatchFromQueue(transaction);
    buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), true);
    return true;
  }
  // reach the maxsize after insert
  auto sibling_new_node = Split(node);
  sibling_new_node->SetNextPageId(node->GetNextPageId());
  node->SetNextPageId(sibling_new_node->GetPageId());
  auto first_key = sibling_new_node->KeyAt(0);
  InsertIntoParent(node, first_key, sibling_new_node, transaction);
  ReleaseLatchFromQueue(transaction);
  leaf_page->WUnlatch();
  buffer_pool_manager_->UnpinPage(sibling_new_node->GetPageId(), true);
  buffer_pool_manager_->UnpinPage(node->GetPageId(), true);
  return true;
}

Remove

和Insert同理，安全条件为不产生合并或者窃取，即删除完至少为半满的状态，条件为 size > MinSize

相关函数：

Remove：入口函数，和Insert一样的处理方式，锁住root_page_latch
- 调用FindLeaf找到对应的叶子节点，此时仍持有叶子节点的锁，
- 如果尝试删除失败，则直接释放叶子节点上的锁，返回
DeleteEntry：
1. AdjustRoot：执行完Remove AdjustRoot函数之后，返回时释放锁即可
2. 无论是Redistribute还是Coalesce，都需要获取到兄弟节点，因此需要对兄弟节点进行加锁

因此，我采用了一种比较无脑的实现方式。即当通过FindLeaf加锁之后，除了之后对兄弟节点进行加锁，其他情况一律不进行加锁，释放锁的操作全部统一到Remove当中，只需要在Remove函数的几次返回时释放锁，对于Delete函数当中，不进行任何解锁操作，Remove函数的大致结构如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void BPLUSTREE_TYPE::Remove(const KeyType &key, Transaction *transaction) {
  root_page_latch_.WLock();
  transaction->AddIntoPageSet(nullptr);
  if (IsEmpty()) {
    ReleaseLatchFromQueue(transaction);
    return;
  }
  // hold the lock of leaf page and unsafe internal page
  auto leaf_page = FindLeaf(key, Operation::DELETE, transaction);
  auto *node = reinterpret_cast<LeafPage *>(leaf_page->GetData());

  if (node->IsLeafPage()) {
    auto before_size = node->GetSize();
    auto size = node->Delete(key, comparator_);
    if (before_size == size) {
      // cannot find the key;
      ReleaseLatchFromQueue(transaction);
      leaf_page->WUnlatch();
      buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), false);
      return;
    }
  }
  auto node_should_delete = DeleteEntry(node, transaction);
  ReleaseLatchFromQueue(transaction);
  leaf_page->WUnlatch();
  if (node_should_delete) {
    transaction->AddIntoDeletedPageSet(node->GetPageId());
  }
  buffer_pool_manager_->UnpinPage(leaf_page->GetPageId(), true);
  std::for_each(transaction->GetDeletedPageSet()->begin(), transaction->GetDeletedPageSet()->end(),
                [&bpm = buffer_pool_manager_](const page_id_t page_id) { bpm->DeletePage(page_id); });
  transaction->GetDeletedPageSet()->clear();
}

UnpinPage

原来在FindLeaf时，一旦遍历至子节点时，当前节点目前就不再被使用，此时就可以对其进行unpin，之所以说目前，是因为后续如果涉及到合并或者重分配到情况，会递归的向上重新获取节点，此时又会在此用到该Page。当时做checkpoint1的时候选择的策略是默认后续不会用到，允许进行淘汰，后续如果需要并且被淘汰了，大不了就再次从磁盘加载，也没什么大不了的。

不过既然实现了并发之后，那么不如将逻辑进行一下统一，如果不安全，那么就既不释放锁，也不进行unpin，等待后续重新使用。封装成一个函数

Think carefully about the order and relationship between UnpinPage(page_id, is_dirty) method from buffer pool manager class and UnLock() methods from page class. You have to release the latch on that page before you unpin the same page from the buffer pool.

并且，根据Lab的提示，需要注意释放锁的顺序和unpind的顺序，这里的锁是加在buffer pool的page上的，如果一个page还未释放掉锁就先unpin，那么之后就有可能被Evict掉，而之后如果需要用到该Page时，再通过FetchPage从磁盘加载，调用构造函数，锁的相关信息就会丢失。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
INDEX_TEMPLATE_ARGUMENTS
auto BPLUSTREE_TYPE::ReleaseLatchFromQueue(Transaction *transaction) -> void {
  while (!transaction->GetPageSet()->empty()) {
    Page *page = transaction->GetPageSet()->front();
    transaction->GetPageSet()->pop_front();
    if (page == nullptr) {
      root_page_latch_.WUnlock();
    } else {
      page->WUnlatch();
      buffer_pool_manager_->UnpinPage(page->GetPageId(), false);
    }
  }
}

除了FindLeaf的FetchPage Unpin之外，其他的就按照checkpoint1当中的实现进行即可，即在Delete的过程当中，对于递归需要的parent page，和合并、重分配需要的sibling page，在哪里Fetch了就在该函数当中进行Unpin即可。

FetchPage和UnpinPage有点像一种资源的申请和释放，可以按照RAII的那种思想，令申请和释放都在同一个作用域内。

Iterator

在Begin当中，通过Findleaf获取到一个leaf_page的锁，之后这个Iterator就一直持有该锁，等到通过++获取到下一个page时，再获取下一个page上的锁，并释放当前page上的锁。通过这种方案确实是能够通过Lab2的测试，但是个人感觉会引起死锁：一个线程正在处理叶子节点的重分配，当前已经获取到了右节点上的锁，正要尝试获取左节点上的锁，而另外一个线程正在执行从左向右的遍历操作，此时获取到了左节点的锁，尝试获取右节点的锁，此时就会形成死锁。这里的处理方式应当为令迭代器进行尝试，如果无法获取锁，那么就放弃获取，并释放掉自身的锁，从而破除死锁。

Debug

多线程debug还是相当头疼的，不过由于我在锁的处理上实现的较为简单，通过FindLeaf获取到锁之后，在Insert和Remove当中只需要在几个地方释放掉锁就可以了，最开始也遇到了一些死锁问题，不过大多都是leaf_page最后忘在正确的地方释放了，通过单线程的单步调试就可以找到卡在了哪里，最终将死锁解决即可。后续再就没有遇见并发安全的问题了，也不存在死锁。个人比较幸运没有出现并发安全的问题，整个过程当中也就没有去一点点读log进行多线程debug。

我个人主要的Bug是存在于checkpoint1当中的delelte的细节没有处理好，checkpoint1在gradescope上的测试并不完善，尤其是对于删除的测试，只进行过最基础的单节点的删除测试，因此在做checkpoint2时存在很多历史遗留问题，最直观的表现为ScaleTest无法通过，即对一个3阶的B+树，进行1w次插入、读取、删除。最后判断是否为空。对于3阶的B+树，插入过程中的分裂非常频繁，删除过程中的合并和重分配也同理。因此如果1w次存在问题，那么就说明B+树的逻辑处理一定存在问题，之后就可以将次数改为10次，运行几次基本上就可以复现1个bug，10次插入删除处理起来也比较方便，通过提供的画图工具把树画出来即可，分析哪里出现了问题。

最后附一个通过记录和Leaderboard

checkpoint2#

Task3#

Task4#

并发#

锁的形式#

Latch Crabbing#

锁的释放#

Search#

Insert#

Remove#

UnpinPage#

Iterator#

Debug#